Взаимното разположение на линия и кръг, платформа съдържание

Относителната позиция на линията и кръга се изясни колко допирни точки и може да има право обиколка в зависимост от тяхната взаимна договореност. Ясно е, че ако линия минава през центъра на кръга, след това пресича периферията на двата края с диаметър, разположена. Това ок.

Нека линия P не минава през центъра О с радиус R на кръга. Направи перпендикулярна на линията ОН и р означават от г дължината на перпендикулярна Т. E, разстоянието от центъра на кръга на линията (фиг. 1). Проучване на взаимното разположение на линия и кръга, в зависимост от съотношението между г и г. Три дела са възможни.

1) г

0B = Следователно точките А и В лежат на окръжност и следователно са общи точки на линия р и определен кръг.

Ние показваме, че линията р и този кръг нямат общ точки. Да предположим, че те имат друга обща точка C. Тогава средната OD-равнобедрен триъгълник SLA. изготвени на основата на АС, е височината на триъгълника, така че ОРП. OD сегменти и не съответстват

тъй като сегментът на средна точка D AC не се изпълнява до точка Н - среден сегмент, AB. Имаме, че от гледна точка О проведе две перпендикулярни: ОН и OD - на линията Р, което е невъзможно. По този начин, ако разстоянието от центъра на кръга на линията на радиус по-малка от обиколката (г <р),топрямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.

2) г = R. В този случай, OH = R, R. Е. Точка Н лежи на кръг, и следователно е обковавам пунктирана линия и кръг (фиг. 1b). Директен кръг р и нямат други общи точки, тъй като за всяка точка M линия стр. Различно от точка Н, ОМ> OH = R (ОМ наклонена вече перпендикулярна OH), и следователно, точка М не лежат на кръга. Така че, ако разстоянието от центъра на окръжността към линията е равна на радиуса на стрейт кръг и има само една обща точка.

3) г> г В този случай, -OH> г така. за всяка точка М 0 М линия р ОН.> R (фиг. 1, а) М Следователно точка не лежат на кръга. Така Ако разстоянието от центъра кръг на линията по-голяма от кръга на радиус, правата линия и кръг са разместени.

Ние сме доказали, че правата и окръжността може да има една или две точки по-чести, а не може да има всякаква обща точка. Права линия като кръг с само една обща точка, наречена допирателни към окръжност, а общата им точка се нарича допирна точка на линията и кръг. На Фигура 2, ред р - допирателна към окръжност с център О и А е точката на допиране.

Ние доказваме, теорема на собственост на допирателната.

Теорема. Допирателната към окръжността, перпендикулярна на радиуса провежда до точката на допиране.

Доказателство. Нека р - допирателна към окръжност с център О. - точката на допиране (виж фигура 2 ..). Ние доказваме. р, че допирателната е перпендикулярна на радиуса ОА.

Да приемем, че това не е така. След ОА на радиус е наклонена към линия стр. Тъй перпендикуляра съставен от точка O до права линия R, е по-малко склонен ОА. разстоянието от центъра О на кръга на линията по-малък от радиуса г. Следователно, линия р и кръгът има две общи точки. Но това противоречи на условието; линия р - допирателната. По този начин, стр линия, перпендикулярна на радиуса ОА. На теоремата се доказва.

Разгледаме две допирателни към окръжност с център O., минаваща през точка А и на обиколката в точки В и С (фиг. 3). Сегментите AB и AC кол сегменти тангента, извлечени от точка А. Те имат свойството, произтичащи от теоремата:

Сегменти до кръга, съставен от една точка, са равни, и правят равни ъгли с линията, минаваща през тази точка и центъра на кръга.

За да докаже това, нека се обърнем към фигура 3. Чрез теоремата на имуществото на тангента ъгли 1 и 2 са прави, така че триъгълниците ABO и ASO правоъгълни. Те са, тъй като те имат една обща хипотенуза ОА и равни краката на ОВ и ОС. Следователно, AB = AC = 3 и 4, както се изисква. Ние сега се докаже теоремата, обратни теореми от свойствата на допирателната (знак на допирателната).

Теорема. Ако линията минава през радиуса на края лежи на окръжността и перпендикулярна на радиуса, допирателна onayavlyaetsya на.

Доказателство. От състоянието на теоремата че радиусът е перпендикулярна съставен от центъра на кръга на дадена линия. Поради това, разстоянието от центъра кръг на линия е равна на радиуса, и следователно, линии и кръгове имат само една обща точка. Но това означава, че линията е до кръга, QED.

Тази теорема се основава решаване на проблеми, за да се изгради тангента.

Директен и обиколка очевидно може само да бъде в следните три относителните позиции:

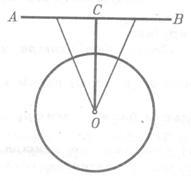
1) Разстояние (OS) от централната линия (АВ) (т. Е OS перпендикулярна дължина, спадна от центъра на права линия) е по-голям от радиуса на окръжността (фиг. 1). След това с права момент е отдалечен от центъра е по-голям от радиуса и затова е извън кръга. Тъй като всички останали точки на линията се отстраняват от около повече от точка С (наклон разстояние перпендикулярно), всички те се намират извън кръга, след това, а направо все още няма общи точки с кръга.

2) Разстояние (OS) на средната линия на по-малък радиус. В този случай (фигура 2), точка С е в кръга и след това, очевидно, линия пресича окръжността.

3> Разстояние (OS) от централната линия равен на радиуса. След точното С (фиг. 3) и принадлежи към правата линия и кръг, всички останали точки на линията, се отстраняват от О повече от точка С лежи извън кръга. Следователно, в този случай, прави линии и кръгове имат само една обща точка, а именно този, който е в основата на перпендикуляра от центъра на права линия.

Такава линия, кръг, който има само една обща точка, наречена допирателната към кръга; обща точка се нарича точката на контакт.

Отнесено към допирателната, се докаже следните две теореми (предна и задна) (Фигура 4):

1) ако линията (MN) е перпендикулярна на радиуса (ОА) в края си (А) лежи на кръг, тя kasaetsyaokruzhnosti и транспорт (Фигура 4) .;

2) ако линия допирателна към окръжността, радиуса, до точката на контакт, перпендикулярно към него.

1) точка А, както е радиусът на края разположена по обиколката на окръжността принадлежи; В същото време той принадлежи към насочи Mn, това означава, че този въпрос е често срещана в кръга и прав. Всички други точки по линията на Mn, като В, С, и други, са разделени от центъра О-далеч от радиуса (като OB на сегменти, OC,. Както наклонена по перпендикулярна ОА), и защото те лежат извън кръга. Така линия MN е само една точка (А), с обща окръжност, и следователно, не е допирателна линия MN а.

2) Ако MN е допирателна към окръжността в точка А, всички останали точки на тази линия трябва да са извън кръга; следователно сегменти ОВ, ОС,. по-голям от ОА на радиус (точка О е центъра на кръга). Така че, това е най-малкият радиус от сегментите, свързващи точка O до всяка точка на линията на Mn, и защото ОА | MN.

Теорема. Ако допирателната е успоредна на акорд, а след това допирна точка разделя дъга, образуван акорд на половина.

Нека линия AB допирателната към окръжността в точка М (Фигура 5.) и успоредна на хордата на CD; изисква да се докаже, че.

Рисуване през точката на допиране диаметър IU. имаме :; следователно

Връзката между арките, акорди и акорд разстояние от центъра.

Теорема. В кръг или в равни кръгове:

1) ако дъгата са равни, а след това затягане си акорди са равни, и на равно разстояние от центъра на града;

2) Ако двете дъги, по-малко от полукръг, не са равни, като повечето от тях се сви с повече акорди и акорди на двете големи намира по-близо до центъра на града.

1) Нека дъга AB е равна на CD дъга (фиг. 1), е необходимо да се докаже, че акорд AB и CD са равни, и равен и вертикалите OE и, намалена от центъра на акорд.

OAJB върти сектора за центъра О в посока на стрелката, така че OB радиус съвпада с операционната система. Тогава дъгата BA. Тя върви по компактдиска с дъга, а заради тяхната равнопоставеност подравняване на дъгата. Следователно, AS акорд съответствие с CD хордата и DE съвпадне с перпендикуляра НА (от една точка може да бъде намалена до само една линия, перпендикулярна) т. Е. AB = CD и OE = НА.

. 2) Да дъга AB (фигура 2) е по-малко от диска на дъга, и, освен това, както дъгата по-малко от полукръг; Необходимо е да се докаже, че акорд AB-малко от компактдиска на акорд, а перпендикулярно OE вече перпендикулярна на. Отлагане SC дъга дъга CD равен на AB, и изготви допълнителен акорд IC. за която е доказано, хорда AB равни и еднакво тя се отстранява от центъра. В COD триъгълници и сок са двете страни на един са равни на две страни на друг (и двете радиуси) и ъглите, сключени между тези страни не са равни; в този случай, както знаем, срещу повече от ъглите, т.е.. д. lCOD, трябва да се основава на по-голямата част, а след това, CD> CK, а защото CD> AB.

За да докаже, че OE> на който, OLXCK провеждане и вземане под внимание това, което е било доказано, OE = OL; Ето защо, ние трябва сравни само с НА ОЛ. В правоъгълен триъгълник 0FM (покрит с фигура инсулти) над крак OM хипотенузата; но OL> ОМ; след това, още по-малко, OL> НА. и защото OE> НА.

Теоремата ни оказа за една обиколка, тя остава валидна при равни кръгове, защото тези кръгове се отличават един от друг само в позицията.

Обратни теореми. Както бе посочено в предишния раздел на всички възможни случаи са взаимно изключващи се по отношение на относителните стойности на двете дъги от същия радиус, където взаимно изключващи станали-заключения по отношение на относителните количества на акорди и техните разстоянията от центъра на града, на предложенията за обратните трябва да се разглежда правилни инча а именно:

В един кръг или д равно кръгове:

1) равни акорди на равно разстояние от центъра и равни затягане на дъгата;

2) акорд, еднакво отдалечени от центъра са равни и еднакво затягане на дъгата;

3) на две неравни акорди голям по-близо до центъра и дърпа голяма дъга;

4) на двете акорди неравномерно, недалеч от центъра, което е по-близо до центъра на града, все повече и дърпа голяма дъга.

Тези предложения могат лесно да бъдат установени със противоречие. Например, за да се окаже първата от тях се мотивира, че ако данните на акорд на дъгата вързани неравно, според прекия теорема не, те щяха да са равни, което противоречи на хипотезата; означава равни акорди трябва да дръпнете равни дъги; но ако дъгата е равен, в съответствие с Direct теорема, затягане на своите акорди са на еднакво разстояние от центъра.

Теорема. Диаметърът е най-великият от акорди.

Ако свържете с центъра на края на всеки акорд, който не минава през центъра, като акорд АБ получаваме триъгълника АОВ, в който една от страните има този акорд, а другите две (Фигура 3). - радиуси, но в триъгълника, всяка страна по-малко от сумата, другите две страни; следователно акорд AB по-малко от сумата на две радиуси; докато всеки CD диаметър е сумата от двете радиуси. Среден диаметър е по-голям, отколкото който и да е на акорд, който не минава през центъра. Въпреки това, тъй като диаметърът е също акорд, може да се каже, че диаметърът е по-голям от акорди.

Както вече беше посочено, сегментите на допирателната към периферията на една точка имат една и съща дължина. Тази дължина се нарича тангенсът разстоянието от точката на обиколката.

Без тангента теорема не освобождава решението не е проблем на вписан кръг, с други думи, на кръг допирателната към страните на многоъгълника.

Тангенциални разстояния в триъгълника.

Намираме дължините на сегментите в който триъгълник ABC страна разделени точки на допиране с кръг вписан в нея (фиг. 1а), като допирателна разстояние та от точка А до кръг. Поставянето Гарнитура за В и С. и след това се изважда количеството на страната на. Като се има предвид равенството на тангенти, съставени от един връх, ние получаваме 2та. По този начин,

където р = (A + B + C) / 2 - половината периметър на триъгълника. Дължината на страните на сегментите в непосредствена близост до върховете Б и В са, съответно, р-б и р-С.

По същия начин, за триъгълника escribed кръг допирателна (извън) страна и (Фиг. 1Ь), на разстояние от тангентата В, и С са съответно р-С и р-Ь. и от горната част A - просто стр.

Имайте предвид, че тези формули могат да се използват "на заден ход".

Да предположим, че ъгъл BAC е вписан кръг, допирателната на разстояние от върха на обиколката ravnop ilip-а на. gdep - половината периметър на триъгълника ABC. и = BC. След кръга е допирателна към линията BC (съответно извън или вътре в триъгълника).

Всъщност, нека, например, разстоянието допирателната е р-а. Тогава нашите кръгове докосват до страните на ъгъла, под една и съща позиция, тъй като вписан кръг на триъгълника ABC. и поради това съвпада с него. Следователно, тя се отнася до прякото Слънцето

Тангенциално четириъгълник. От теоремата на равенството на тангенциалната веднага получава (фиг. 2а), че

Ако четириъгълник е възможно да се впише в кръг, след това сумата от неговите срещуположни страни са равни:

Имайте предвид, че допирателна четириъгълник задължително изпъкнал. Обратното е вярно:

Ако изпъкнал четириъгълник и размера на неговите срещуположни страни равни, тогава кръг може да се впише в него.

Нека да докажат това на четириъгълник, различна от успоредник. Нека всеки две противоположни страни на четириъгълник, например AB и DC, като продължава да се пресичат в точка Д (фиг. 2Ь). Впише окръжност в триъгълника ADE. Разстоянието ТЕ допирателната в точката Е се изразява чрез формулата

Но състоянието на размера на срещуположните страни на четириъгълник са равни, и по този начин, AD + BC = AB + CD. или AD = AB + CD-BC. Заместването на тази стойност в израза за ТЕ. получаваме

и това - времето на периметъра на триъгълника BCE. От условието се оказа по-горе трябва да пипате, че нашият кръг е допирателна към Христа.

Две допирателна към кръга от точка извън него, са равни и образуват равни ъгли с линия, свързваща тази точка до центъра, която следва от уравнение правоъгълен триъгълник АОВ и AOV1 на