Решаване на системи линейни уравнения от Гаус-Йордания

Като цяло, линейното уравнение е:

Уравнението има решение: ако поне един от коефициентите на неизвестните не е нула. В този случай, всеки измерен вектор, наречен разтвор на уравнение ако уравнение става идентичност чрез заместване на неговите координати.

Обща характеристика на разделителната способност на системата от уравнения

За да се характеризират системата от уравнения.

1. е е част от система от линейни уравнения противоречива уравнение? (Ако коефициентите, в този случай уравнение има формата и се нарича несъвместими.)

• Ако системата съдържа противоречиви, такава система е в противоречие и няма решения

2. Намерете всички разрешени променливи. (Файл nazyvaetsyarazreshennoy за системата, ако е включен в една система от уравнения с коефициент на 1, а в други уравнения не е включена (т.е., влиза фактор равна на нула).

• В нашия пример, неизвестен част от първото уравнение с коефициент единица, второто уравнение не е включена, т.е. първо се оставя.
• По същия начин - да се открие само през второто уравнение и само в първата.

3. Системата за издаване на разрешително от уравнения? (Наречен разрешено системата от уравнения. Ако всеки уравнение съдържа оставя неизвестен, сред които няма припокриване)

• Нашата система е допустимо, тъй като всеки уравнение съдържа оставя неизвестен)

Разрешена неизвестен, взето по един от всяка уравнение на системата, се образува пълен комплект позволено неизвестен система. (В този пример)

Разрешени неизвестни срещащи се в пълен комплект, наречен също основните () не са включени в комплекта - безплатно ().

В общи линии, разделителната способност на системата уравнения е от вида:

На този етап най-важното да се разбере какво е позволено неизвестен (част от базата и безплатно).

Общо Частно основно решение

Общото решение на системата разрешено е колекция от изрази, допускат непознати чрез свободните условията и свободни неизвестни:

Особено разтвор на системата е разтвор, в резултат от общото при конкретните стойности на свободните променливи и неизвестни.

Основният разтвор се нарича специално разтвор, в резултат от общата при нулеви стойности на свободните променливи.

• Основен разтвор (вектор) се нарича изроден. ако броят на неговия произход, различен от нула, по-малко от броя на позволено неизвестен.
• Основен разтвор се нарича не-дегенерат. ако броят на неговия произход, различен от нула, равен на броя на позволено неизвестен система, включена в пълен комплект.

Теорема (1)

Разрешена система от уравнения винаги е в съответствие (тъй като тя има поне едно решение); и ако системата не е без неизвестни (т.е. системата от уравнения включва всички допуснати в основата) се определя (има уникално решение); ако има поне една свободна променлива, тогава системата не е определено (има безкрайно много решения).

Пример 1. Намери цяло, основно, и всяко конкретно решение на системата от уравнения:

1. Проверете дали разделителната способност на системата?

• Системата се оставя (като всеки от уравнения съдържа оставя неизвестен)

2. Включете в комплекта позволено неизвестно - по един от всяка уравнение.

• В нашия случай, ние можем да се включат в комплект позволено неизвестно от първото уравнение - и, както само от второто уравнение. Това означава, че набор може да се състои от () и ().

3. Напишете общото решение, в зависимост от това, което разрешения не са известни, ние сме включени в комплекта.

• да кажем, че сме включили набор от неизвестни и след общото решение ще изглежда така:

4. Намерете конкретно решение. За да направите това, ние се равнява на свободните променливи, че не сме включени в комплекта, до сумата на произволен брой.

• Да предположим, тогава общото решение е намерена:

Отговор: специално разтвор (един)

5. Ние считаме, основното решение. За да направите това, ние се равнява на свободните променливи, че не сме включени в комплекта на нула.

Начални линейни уравнения трансформация

линейна система уравнения са разрешени за еквивалентни на системи, използващи елементарни трансформации.

Теорема (2)

Ако някоя уравнение система се умножава с различен от нула номер. а останалите уравнения остават непроменени, ние получаваме системата е еквивалентно на това. (Това означава, че ако умножим лявата и дясната страна на уравнението на същия номер, можете да получите едно уравнение, еквивалентно на това)

Теорема (3)

Ако по някаква уравнение на системата, за да добавите повече. и всички останали от уравнението остане непроменена, ние получаваме системата е еквивалентно на това. (Това означава, че ако добавим двете уравнения (сумата от левия и десния хълбок), ние получаваме уравнение равностойни данни)

Следствие на теория (2 и 3)

Ако по някаква уравнение да добавите друг умножена по някакъв номер. и всички останали от уравнението остане непроменена, ние получаваме системата е еквивалентно на това.

Формула преизчисляване на коефициентите

Ако имаме система от уравнения, и ние искаме да го превърне в система от уравнения ни позволи да помогне в този метод на Гаус-Джордан.

Трансформация на Йордания толерантен елемент позволява да се получи система от уравнения за неизвестното в уравнение допуска в стаята. (Пример 2).

Трансформация на Йордания се състои от елементарни преобразувания на два типа:

1. Уравнение толерантен елемент се разделя на този елемент (умножена по)
2. Уравнение толерантен елемент се умножава по съответния фактор, и се добавя към всички други уравнения за премахване на непознатото.

Да кажем, че ние искаме да направим неизвестното в долния уравнение допуска неизвестен. За да направите това, трябва да бъде разделена на, така че сумата.

ПРИМЕР 2 преизчисли коефициентите

При разделяне на уравнение с броя на неговите коефициенти се преизчисляват съгласно формулите:

да се изключат

от уравнение с индекс , Имаме нужда от едно уравнение с много умножена с и се прибавя към уравнението.

Теорема (4), за да се намали броят на уравнения.

Ако системата от уравнения съдържа тривиално уравнение, може да се отстранява от системата, като по този начин се получи система еквивалентна на оригинала.

Теорема (5) несъвместимостта на уравнения.

Ако системата от уравнения съдържа противоречива уравнение, което е несъвместимо.

Алгоритъмът на метода на Гаус-Jordan

Алгоритъмът за решаване на системи уравнения от Гаус-Иордан се състои от серия от подобни стъпки, всяка от които изпълнява действия в следния ред:

1. Проверени, не е в противоречие система. Ако системата съдържа противоречива уравнение, което е несъвместимо.
2. Проверени възможността за намаляване на броя на уравнения. Ако системата съдържа тривиално уравнение, си стачка навън.
3. Ако системата от уравнения е решен, след това да напишете общото решение на системата и, ако е необходимо - частни решения.
4. Ако не е позволено на системата, след това в уравнението, не съдържащ неизвестно разрешено, позволявайки избран елемент и произвеждат превръщане Jordan с този елемент.
5. По-нататък отново прехвърля в параграф 1,

Пример 3 За решаването на системата от уравнения от Гаус-Jordan.

Намери. две цяло и две съответни основни разтвори

Изчисленията дадени в следната таблица:

Вдясно от таблицата показва действията на уравненията. Стрелките показват, към който се добавя уравнение уравнение толерантен елемент умножена по подходящ фактор.

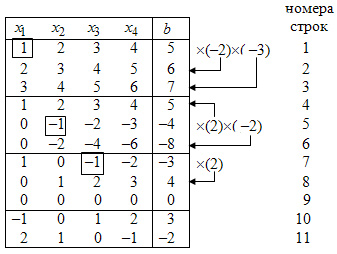
През първите три реда от таблицата са поставени коефициентите на непознатото и дясната страна на оригиналната система. Резултатите от първата реализация елемент Jordan толерантен единството показани на линии 4, 5 и 6. Резултатите от втория елемент превръщане Jordan толерантен равна на (1) са показани на линии 7, 8, 9. Тъй като третата уравнението е тривиално, не може взети под внимание.

Еквивалентно система допуска неизвестен и има следния вид:

Сега можем да пишем общото решение:

Ние приравняваме свободни променливи и нула и получаваме.

За да намерите втория генерала и съответния основен разтвор, в резултат на резолюцията на системата във всеки уравнение трябва да изберете всеки друг елемент, който позволява. (Фактът, че линейното уравнение може да включва някои общи и основни разтвори). Ако разделителната способност на системата от уравнения е еквивалентно на оригиналната система съдържа неизвестни и уравнения, броят на обикновените и съответните решения на базата на оригиналната система е броят на комбинации и. Броят на комбинации може да се изчисли по формулата:

В нашия случай, ние са избрани позволява елемент (1) в първото уравнение за (линия 7). Следваща е превръщането на Jordan. Има нов (линии 10-11) допускат в нова система допускат неизвестни:

Напишете втората общото решение:

И съответния основен разтвор.