Разстоянието между кос линии
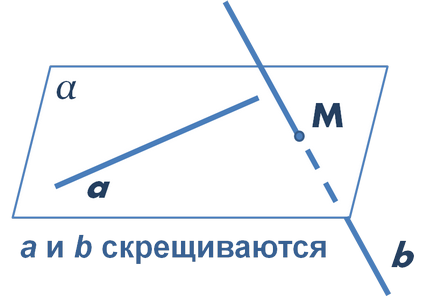
В тази статия пример за решаването на проблема с С2 УПОТРЕБА разглоби метод за намиране на разстоянието между редовете кос чрез координиране метод. Спомнете си, че линиите са skreschivayuschi-Мизия, ако те не лежат в една равнина. По-специално, ако една линия лежи в равнина, а втората права линия пресича тази равнина в точка, която е разположена на първия права линия, тези прави линии са кос (вж. Фигура).
За да намерите разстоянието между кос линии следва:
- Чрез директно един от кос равнина, която е успоредна на останалите кос линии.
- Долна перпендикулярна от всяка точка на втората права линия, получена равнина. Дължината на перпендикулярите ще бъде желаното разстояние между линиите.
Нека разгледаме алгоритъма в подробности по примера на решаването на проблема с изпита по математика C2.
Разстоянието между правите линии в пространството
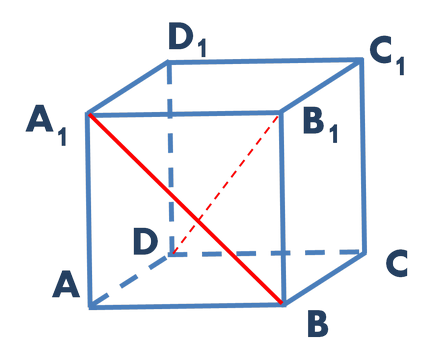
Фиг. 1. планира да задача
Решение. DB1 диагонално през средата на куб (O точка) на нарисувате права линия, успоредна на a1b на линия. Точките на пресичане на права линия BC и A1D1 ребрата съответно обозначени N и М. Direct MN MNB1 лежи в равнина, успоредна на линията и А1В. която в този самолет не лъже. Това означава, че линията е успоредна А1В MNB1 равнина на базата на успоредната линия и равнина (фиг. 2).
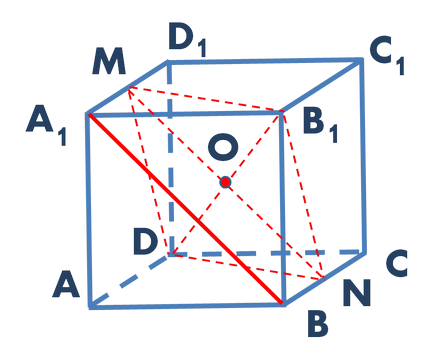
Фиг. 2. необходимото разстояние между кос линии равна на разстоянието от всяка точка на избраната линия на равнината на изображението
Търсим сега разстоянието от всяка една точка на линията, за да равнина A1B MNB1. Това разстояние ще бъде по дефиниция е желаното разстояние между кос линии.
За да се определи това разстояние чрез използване на координатите. Представяме правоъгълна Декартова координатна система, така че неговия произход съвпада с точка Б, X ос е насочена по ръбовете BA. заедно ръб BC - Y ос. ос Z - заедно ВВ1 на ръба (фигура 3.).
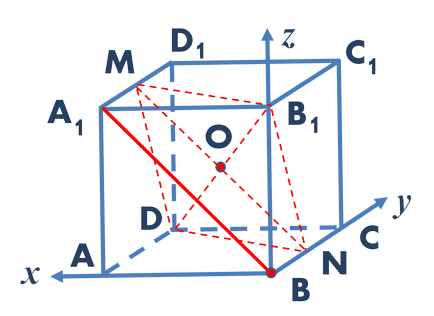
Фиг. 3. правоъгълна Декартова координатна система е избрана така, че както е показано на фигура
MNB1 намери уравнението на равнината координатна система. За тази координатите на точките определят първи М. N и В1. Полученото координира заместител в общото уравнение на права линия и се получи следната система от уравнения:
От второто уравнение получаваме от третото получаваме след това от първа получи Замествайки стойностите, получени в общото уравнение на линия:
Забелязваме, че в противен случай би MNB1 самолет преминава през началото. Разделяме двете страни на това уравнение върху и да получите:
Разстоянието от гледна точка на равнината, определена от формулата:
където - координатите на точка В. - коефициентите на променливите в уравнението на самолета. Точка Б има координати най-накрая да получат: