Нормалното разпределение (Гаусово разпределение)

Апаратурата на математическата статистика е сравнително добре развита по отношение на състоянието, когато разпределението на случайната променлива подчинява нормално разпределение (закон на Гаус).

Проучванията при машиностроенето са установили, че по-голямата част от характеристиките на технологичните процеси то е предмет на този закон.

Нормално разпределение играе решаваща роля във всички области на техническите науки, и заема особено място сред другите закони на разпределение.

Нормално разпределение на случайната променлива възниква в случаите, когато резултатът от теста е следствие от редица фактори, сред които не са доминиращи, а обемът на наблюдение е достатъчно голям. Много непрекъснат мониторинг с увеличаваща се сила тест клони към нормалното разпределение.

Случайна променлива има нормално разпределение, ако уравнението на функцията на плътността на вероятността е:

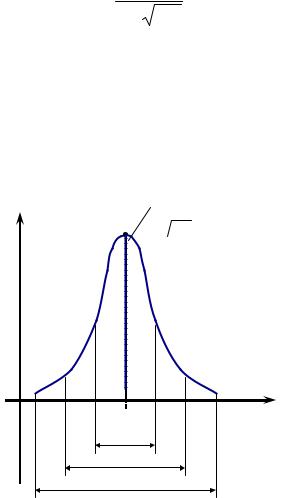
Теоретичната кривата на закона на нормално разпределение е с форма на камбана, симетрични по отношение на перпендикуляра към оста х, минаваща през точка на оста х с Y координата на. Тя достига максимум в този момент (0 1 σ 2 π) асимптотично подходи нула

Очакванията: M (Y) = Y 0. дисперсия: D (Y) = σ 0 2.

Площта под кривата ограничен интервал Y 1 ≤Y ≤Y 2. 0 съответства на вероятността, че експерименталните резултати ще падне в гнездото. В рамките на ± 3σ от 0 Y е 0 99,73% от площта под кривата.

Ето защо, на практика за нормалното разпределение се използва "три сигма правило". Защото законът на нормално разпределение на базата на "правилото за три сигма", стр разсейване поле на случайната променлива е:

р = (Y о + 3 σ О) - (Y о - 3 σ о) = 6 σ о.

Поради факта, че цената сигма 0 и х 0, като се използват характеристиките на S на пробата и X, практически бездомни поле се определя от формулата:

където L - коефициент стойност маса приема за даден размер на проба за α = 0,95 (където L се изчислява от условието, че броят на случайни променливи, които са в областта бездомни практическото е 99.73%).

Примери на нормалното разпределение са:

- разпределението на грешката на измерване;

- измерване характерен параметър в същата партида на продуктите;

- позициониране грешка на металорежещи машини с ЦПУ, роботи и т.н.