лежащи в една равнина вектори

Две вектори са успоредни една и съща равнина, се наричат ​​в една равнина.

Да предположим, че са ни дадени три вектора $ \ overrightarrow, \ \ overrightarrow $ и $ \ overrightarrow $. след това

Чифт вектори $ \ overrightarrow \ и \ \ $ overrightarrow, $ \ overrightarrow $ и $ \ overrightarrow $ и $ \ overrightarrow $ и $ \ $ overrightarrow копланарни един с друг.

Ако две от тези вектори, като например $ \ overrightarrow, \ и \ \ $ overrightarrow, лежат на една права, то векторите $ \ overrightarrow, \ \ overrightarrow $ и $ \ $ overrightarrow една равнина.

Ако $ \ overrightarrow, \ \ overrightarrow $ и $ \ $ overrightarrow намират в една и съща равнина, те са в една равнина.

За по-нататъшно разглеждане ние си спомняме следната теорема.

Произволен вектор $ \ overrightarrow

$ Може да се разшири в две не-колинеарни вектори $ \ overrightarrow \ $ и $ \ $ overrightarrow само с коефициентите на разширение, т.е.

Теореми, свързани с концепцията за успоредностмежду на три вектора

Нека там да се даде една кутия. Намери тройна копланарни вектори, изобразени на паралелепипеда на фигурата по-долу.

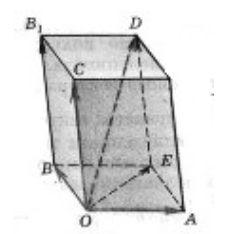
От $ на вектори \ overrightarrow, \ \ overrightarrow $ и $ \ $ overrightarrow лежат в равнината $ (БОА) $ тогава тези вектори са в една равнина.

Тъй като вектори $ \ overrightarrow, \ \ overrightarrow $ и $ \ overrightarrow_1> $ лежи в равнината $ (ВОС) $ тогава тези вектори са в една равнина.

От $ на вектори \ overrightarrow, \ \ overrightarrow $ и $ \ $ overrightarrow лежат в равнината $ (СЕ) $ тогава тези вектори са в една равнина.

Докаже, че векторите с координати $ \ наляво (1 \ 13 \ 2 \ полето), \ \ оставени (3 \ -5 \ 2 \ вдясно) и \ (5, 1,4) $ една равнина.

Ние прилагаме знака на една равнина на три вектора.

Поради това е от една равнина вектори.