Lagrange метод множител - studopediya

LP и НЛП проблеми са решени в една стъпка. Тези проблеми се наричат ​​един етап (от същия тип). Дийн задача. Pr. наречен многоетапно - на всеки етап се определя от решението на някои части от задачите, причинени първоначалния проблем.

Общият състав на целите DP. Нека физическата система S е в начален състояние S0 Je Snach. и е управляема. Благодарение на някои упражнения. U, системата се премества от първоначалното състояние на крайния състоянието S0 Skon. Skon Je SK.

По този начин, тъй като всеки от контролите U се характеризира със съответната стойност на W функция (U).

Предизвикателството е да се установи множество контроли, в които W функция (U) се крайна стойност.

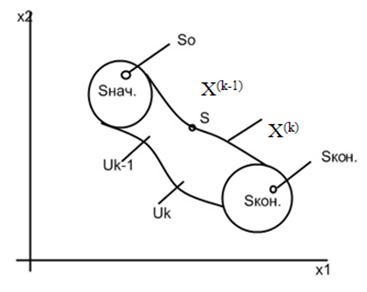
решаване на ДП проблем се извършва по схемата:

Предполагаме, че състоянието на разглеждания S система, в която к - стъпка m, с к = 1 ... п определя от комбинация от числа X (к) = (X1 (к) х2 (к) ... Xn (к) ..), които са получени Великобритания резултат на системата за контрол осигурява преход Siz състояние X (к-1) до състояние х (к).

Предполага се, че държавната Х (к), зависи от държавния Х (к-1) и избраната контрола Великобритания, но не зависи от начина, по който системата S е преминал в това състояние.

Разрез. За изпълнение на първия етап се получава печалба състояние зависи от предх. състояние (X (к-1)) и Великобритания уравнение.

Общият принос в този случай ще бъде:

F = Σ Wk (X (к-1), Великобритания)

DP за решаване на проблемите на такава схема се извършва в съответствие с принципа на оптималност Bellmona.

Изявление: какво би било състоянието на системата преди следващата стъпка трябва да бъде следващата стъпка е да се избере за контрол, така че ползата от тази стъпка, плюс оптималната печалба при всички следващи стъпки е максимално.