Емпиричните функция на разпределение - studopediya

Определяне 25.2.Empiricheskoy разпределение функция извикване на функция (функция за вземане на проби) определяне за всяка стойност на относителната честота на събитието, т.е.

където - няколко по-малки; - размер на пробата.

От теоремата на Бернули следва, че за достатъчно голям размер на извадката и функции се различават малко от един на друг. За разлика разпределение функция на теоретичната емпиричната е, че функцията на теоретичното разпространение определя вероятността на събитието и емпирична функция определя относителната честота на същото събитие.

Емпиричните функция разпределение притежава всички свойства кумулативната функция разпределение:

1) стойности на функцията за емпирична разпределение принадлежат към сегмента;

2) - не-намаляване функция;

3) ако - най-малката изпълнение, когато; ако - най-големият вариант, когато.

Пример 25.1. За да се конструира емпирична функция разпределение в тази проба:

Решение. Ние считаме, размер на пробата: 12 + 18 + 30 = 60.

2. Следователно ниската изпълнение е.

Стойност, а именно, че е 12 пъти, следователно с.

Стойност, а именно, и се наблюдават 12 + 18 = 30 пъти, следователно, когато.

Тъй като - най-големият вариант, когато.

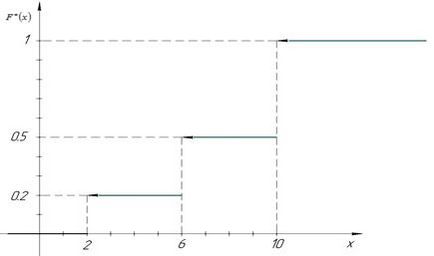
Вие емпиричната функция

Графиката на тази функция е както следва: