Basic (ядро) и безплатна (второстепенни) променливи
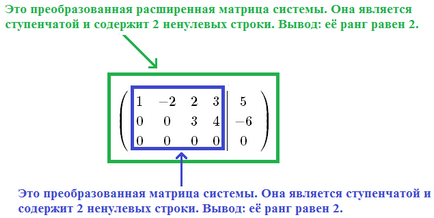
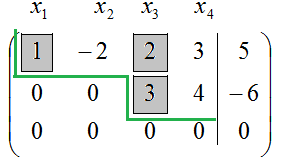
Темата "Кронекер-Капели Теорема", беше заявено, че ако ранга на разширяване матрица система $ \ widetilde $ ранг и матрица на системата за $ A $ са равни, тогава дадената система от линейни алгебрични уравнения (SLAE) съвместими, т.е. Той има решение. Въпросът за броя на решенията, активирани с разследването на Кронекер. Според него, ако $ \ звънна A = \ звънна \ widetilde = п $ ($ п $ - брой неизвестни), че Слоу има уникално решение. Ако $ \ звънна A = \ звънна \ widetilde От особен интерес е звънна случай на $ \ A = \ звънна \ widetilde Какво означава изразът "в ранг е равен на $ R $"? Това означава, че има най-малко един Мала $ R $-ти ред, който не е нула. Спомням си, че непълнолетен, се нарича основа. Основа на непълнолетните могат да бъдат няколко. По този начин всички непълнолетни, чиято цел е над $ R $, са равни на нула или не съществува. Ако коефициентите на променливите $ R $ за да формират заедно SLAE основа непълнолетен матрица система $ A $, а след това тези променливи $ R $ нарича основна или фундаментален. Останалите $ п-R $ променливи, наречени свободни или не-ядро. $ R $ Изберете основни променливи като цяло могат да бъдат най-различни начини. В примерите ще покажа най-често използваният метод на избор. Решение Слау. при което всички свободни променливи са равни на нула, наречена база. Във всички по-долу примери, матричната система е обозначен с $ A $ и разширената матрица на системата - писмо $ \ widetilde $ на. Решете линейни системи $ \ ляво \<\begin & 3x_1-6x_2+9x_3+13x_4=9\\ & -x_1+2x_2+x_3+x_4=-11;\\ & x_1-2x_2+2x_3+3x_4=5. \end \right.$. Если система является неопределённой, указать базисное решение. Така че, ние имаме линейни системи, които има 3 уравнения и 4 променливи: $ x_1 $, $ x_2 $, $ x_3 $, $ x_4 $. Тъй като броят на променливите е по-голям от броя на уравненията, такава система не може да има уникален разтвор (малко по-късно ние стриктно се окаже предложението въз основа на Кронекер-Капели). Slough намери решения, използващи Гаус: $$ \ ляв (\ започне 3 -6 9 13 9 \\ -1 2 1 1 -11 \\ 1 -2 2 3 5 \ край \ вдясно) \ стрелкаНадясно \ лява | \ започне \ Текст \\ \ Текст \\ \ Текст \ край \ десен | \ СтрелкаНадясно \\ \ стрелкаНадясно \ ляв (\ започне 1 -2 2 3 5 \\ -1 2 1 1 -11 \\ 3 -6 9 13 9 \ край \ дясно) \ започне \ фантом \\ II + I \\ III-3 \ cdot I \ край \ стрелкаНадясно \ наляво (\ започне 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 3 4 -6 \ край \ дясно) \ започне \ фантом \\ \ фантом \\ III-II \ край \ стрелкаНадясно \\ \ стрелкаНадясно \ наляво (\ започне 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 0 0 0 \ край \ вдясно) $$ Приключихме напред хода на метода на Гаус, с което усилва матрица на системата да ешелон форма. Вляво от функциите са елементи на матрицата на системата се трансформира, ние също са довели до ешелон форма. Позволете ми да ви напомня, че ако им се даде определена матрица, за да ешелон форма, а след това му ранг е равен на броя на ненулевите редове. И матрицата система и разширена система матрица след еквивалентни преобразувания са намалени до ешелон форма; Те съдържат два не-нулева линия. Заключение: $ \ звънна A = \ звънна \ widetilde = 2 $. По този начин, тъй SLAE включва четири променливи (означени като номер $ п $, т.е. $ п = 4 $). Освен това, системата е на системата и разширената матрица на матрицата са равни една на друга и е равен на броя на $ г = 2 $. От $ R Ние считаме тези решения. За да започнете, изберете основните променливи. Техният брой трябва да е равно на $ R $, т.е. в нашия случай, ние имаме две основни променливи. Какви променливи (защото ние ги имаме 4 броя) да се приемат като основа? Обикновено, основните променливи вземат тези променливи, които са разположени на първите места в различни от нула, редовете на матрицата се трансформира на системата, т.е. на "стъпки". Какво е това "стъпка" е показан по-долу: На страницата "стъпки" са на броя на колоните №1 и №3. Първата колона съответства на променливата $ x_1 $, а третата колона съответства на променливата $ x_3 $. Това променливи $ x_1 $ и $ $ x_3 вземе като база. Защо да приемаме променливите $ x_1 $ и $ $ x_3 като основа? За да отговорим на този въпрос, нека си припомним, че рангът на системата е броят на $ R = 2 $. Той казва, че всички непълнолетни на тази матрица. За да е по-голямо от 2, или равна на нула, или не съществува. Различна от нула непълнолетни лица сред малолетните имат само втори ред. Ние избираме всеки ненулев непълнолетен втори ред. Можем да го изберете като в първоначалната матрица система $ $ А, т.е. в матрица $ \ наляво (\ започне 3 -6 9 13 \\ -1 2 1 1 \\ 1 -2 2 3 \ край \ вдясно) $, а трансформира система матрица, т.е. в $ \ ляво (\ започне 1 -2 2 3 \\ 0 0 3 4 \\ 0 0 0 0 \ край \ вдясно) $. Тъй като трансформира матрицата повече нули на системата, а след това той ще работи с него. Така че нека да избере втори ред дребни елементи, които са в пресечната точка на линиите №1 и №2, както и колони №№ 1 и № 2: Заключение: избран контакт Мала втори ред не е основен, тъй като тя е нула. Тъй като елементите на тази малка се вземат от колоната №1 (това съответства на променливата $ x_1 $) и колона №2 (това съответства на променливата $ x_2 $), след това двойката променливи $ x_1 $ и $ $ x_2 не може да бъде основни променливи. Направи втори опит, като по-маловажни елементи от втори ред са разположени в пресечната точка на линии №№ 1, №2 и колони №2 и №4: Заключение: избрания контакт е непълнолетен втора база ред, тъй като не е нула. Тъй като елементите на тази незначителна се вземат от колоната №2 (тя отговаря на променливата $ x_2 $) и колона №4 (тя отговаря на променливата $ x_4 $), няколко променливи x_2 $ $ и $ $ X_4 може да се вземе за основа. Да направим трети опит и намиране на стойността на непълнолетния, елементите от които се намират в пресечната точка на линиите №1, №2 и №3 колони №1 и: Заключение: избрания контакт е непълнолетен втора база ред, тъй като не е нула. Тъй като елементите на тази незначителна се вземат от колоната №1 (тя отговаря на променливата $ x_1 $) и колона №3 (тя отговаря на променливата $ x_3 $), няколко променливи $ x_1 $ и $ $ x_3 може да се вземе за основа. Както можете да видите, изборът на основните променливи не е еднозначен. В действителност броят на избор е не по-висок от броя на разположения от $ N $ елементи $ R $, т.е. не повече от $ C _ ^ $. В този пример, тъй като baisnyh бяха приети променливи $ x_1 $ и $ x_3 $ - чисто за по-голямо удобство на по-нататъшни решения. Какво е това удобство, ще видим малко по-късно. Основни променливи са избрани: тя е $ x_1 $ и $ x_3 $. Останалите $ п-R = 2 променливи $ (т.е. $ x_2 $ и $ x_4 $) са свободни. Трябва да изразим основните променливи чрез безплатно. Аз предпочитам да работя със системата в матрична форма. За да започнете да чистя получената матрица $ \ ляво (\ започне 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 0 0 0 \ край \ вдясно) $ от нулевата линия: $$ \ ляв (\ започне 1 -2 2 3 5 \\ 0 0 3 4 -6 \ край \ вдясно) $$ Безплатни променливи, т.е. $ X_2 $ и $ x_4 $, съответната колона №2 и №4. Бързо напред тези колони над линията. Влезте всички елементи, носени от колоната ще се промени на обратното:
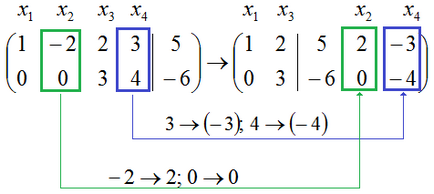
Защо получавам знаците? Какво означава всичко това прехвърляне на колони? Покажи \ скрий
Нека се обърнем към матрицата на удължения система, която след преобразуването е на форма $ \ наляво (\ започне 1 -2 2 3 5 \\ 0 0 3 4 -6 \ край \ вдясно) $. Нека да преминем към уравненията на матрицата. Първият ред съответства на уравнението $ x_1-2x_2 + 2x_3 + 3x_4 = $ 5 и втора линия съответства на уравнението $ 3x_3 + 4x_4 = -6 $. Сега прехвърляне на свободните променливи x_2 $ $ и $ $ X_4 в страните на дясната страна на уравнения. Разбира се, когато се движим изразът $ 4x_4 $ в дясната страна на уравнението, знак, че ще се промени в обратното, а от дясната страна ще бъде $ -4x_4 $.
\ започне x_1 + 2x_3 = 5 + 2x_2-3x_4; \\ 3x_3 = -6-4x_4. \ край
Ако отново да записва получената система под формата на матрица, ние получаваме една матрица с колони се премества над линията.
И сега ние продължаваме справяне обичайния метод на Гаус. Нашата цел: да се направи матрица за характеристиките на устройството. За да започнете, се разделят на втория ред с 3, а след това продължи да се превърне обратно метод заместване:
$$ \ ляв (\ започне 1 2 5 2 -3 \\ 0 3 -6 0 -4 \ край \ дясно) \ започне \ фантом \\ II: 3 \ край \ стрелкаНадясно \ наляво (\ започне 1 2 5 2 -3 \\ 0 1 -2 0 -4/3 \ край \ вдясно) \ започне I-2 \ cdot II \\ \ фантом \ край \ стрелкаНадясно \\ \ стрелкаНадясно \ ляво (\ започне 1 0 9 2 1/3 \\ 0 1 -2 0 -4/3 \ край \ вдясно). $$
Хотелът матрица, за да се превърне в единна, завършена Гаус. Общото решение е установено, остава само да го напиша. Ако си припомним, че четвъртата колона съответства на променливата $ x_2 $, а петата - променлива $ $ X_4, получаваме:
Ние получава общото решение даден SLAE. За да намерите основния разтвор, трябва всички свободни променливи се равняват на нула. Т.е. приемайки $ x_2 = 0 $ и $ x_4 = 0 $, ние имаме:
Разтвор $ x_1 = 9 $, $ x_2 = 0 $, $ x_3 = -2 $, $ x_4 = 0 и $ е база решение на този SLAE. По принцип, за определяне на свободните променливи други стойности, които можете да получите други конкретни решения на тази система. Такова лично безкраен брой решения. Например, като $ x_2 = -4 $ и $ x_4 = 1 $, ние получаваме конкретен разтвор: $ \ ляво \ x_1 = \ Frac; \\ x_2 = -4; \\ x_3 = - \ Frac; \\ x_4 = 1. \ Край \ прав. $. Основен разтвор, който ние открихме по-рано - само един от безкраен брой конкретни решения даден Слау.
Ако желаете, полученият разтвор може да бъде проверена. Например, замествайки $ x_1 = 9 + 2x_2- \ fracx_4 $ и $ x_3 = -2- \ fracx_4 $ в лявата страна на първото уравнение, ние получаваме:
$$ 3x_1-6x_2 + 9x_3 + 13x_4 = 3 \ cdot \ наляво (9 + 2x_2- \ fracx_4 \ дясно) -6x_2 + 9 \ cdot \ наляво (2- \ fracx_4 \ дясно) + 13x_4 = 9. $$
Проверка на първо уравнение неуспешен; по същия начин, можете да проверите на втория и третия уравнения.
Отговор. Общото решение: $ \ лява \ x_1 = 9 + 2x_2- \ fracx_4; \\ x_2 \ в R; \\ x_3 = -2- \ fracx_4; \\ . X_4 \ в Р. \ край \ прав $, основно решение е: $ \ лява \ x_1 = 9; \\ x_2 = 0; \\ x_3 = -2; \\ x_4 = 0. \ Край \ прав. $.
Решете линейни системи $ \ ляво \ x_1-2x_2 + 4x_3 + 2x_5 = 0; \\ 4x_1-11x_2 + 21x_3-2x_4 + 3x_5 = 1; \\ -3x_1 + 5x_2-13x_3-4x_4 + x_5 = -2. \ Край \ прав. $. Ако системата не е сигурен, посочва основния решение.
Подобен пример вече е решен в "метод на Kramer" обект линия (пример №4). Променливите $ X_4 $ и $ x_5 $ са прехвърлени на страните на дясната ръка, а след това се използва стандартен метод на работа Крамер. Въпреки това, този метод не гарантира решения за постигане на резултати. Например, ние носим някои променливи в дясната ръка, а останалите определящ фактор е равен на нула, - тогава какво? Брутална сила за решаване. ) Поради това е много по-удобно да се използва за трансформация на метода на Гаус. както в предишния пример.
$$ \ ляв (\ започне 1 -2 4 0 2 0 4 \\ -11 21 -2 3 -1 \\ -3 5 -13 -4 1 -2 \ край \ дясно) \ започне \ фантом \\ II-4 \ cdot I \\ III + 3 \ cdot I \ край \ стрелкаНадясно \ наляво (\ започне 1 -2 4 0 2 0 \\ 0 -3 5 -2 -5 -1 \\ 0 -1 -1 -4 7 -2 \ край \ вдясно) \ стрелкаНадясно \\ \ стрелкаНадясно \ лява | \ започне \ Текст \\ \ Текст \\ \ Текст \ край \ дясна | \ стрелкаНадясно \ ляво (\ започне 1 -2 4 0 2 0 \\ 0 -1 -1 -4 7 -2 0 \\ -3 5 -2 -5 -1 \ край \ дясно) \ започне \ фантом \\ \ фантом \\ III-3 \ cdot I \ край \ стрелкаНадясно \\ \ стрелкаНадясно \ наляво (\ започне 1 -2 4 0 2 0 \\ 0 -1 -1 -4 7 -2 0 \\ 0 8 10 -26 5 \ край \ вдясно). $$
Системата за матрица и напреднал матрицата на системата се намалява до трапецовидна форма. Степени на тези матрици са равни една на друга и е равен на броя 3, т.е. $ \ Rang A = \ звънна \ widetilde = 3 $. От редиците са равни или по-малко от броя на променливите, според разследването на Кронекер-Капели тази система има безкраен брой решения.
Броят на неизвестни $ п = 5 $, в редиците на двете матрици $ R = 3 $, така че трябва да изберете три основни променливи и $ п-р = $ 2 безплатни променливи. Прилагайки същия метод "стъпки", както в предишния пример, ние избираме като основните променливи $ x_1 $, $ x_2 $, $ x_3 $, както и свободните променливи - $ x_4 $ и $ x_5 $.
Колони №4 и №5, които съответстват на свободните променливи, превъртане напред над линията. След разделяне на третата линия 8 и увеличи разтвор метод Гаус:
$$ \ ляв (\ започне 1 -2 4 0 0 -2 0 \\ -1 -1 -2 4 -7 \\ 0 0 8 5 -10 26 \ край \ вдясно) \ започне \ фантом \\ \ фантом \\ III: 8 \ край \ стрелкаНадясно \ ляво (\ започне 1 -2 4 0 0 -2 0 \\ -1 -1 -2 4 -7 \\ 0 0 1 5/8 -5/4 13/4 \ край \ дясно) \ започне I-4 \ cdot III \\ II + III \\ \ фантом \ край \ стрелкаНадясно \\ \ наляво (\ започне 1 -2 0 -5/2 5 -15 \\ 0 -1 0 -11/8 11/4 -15/4 \\ 0 0 1 5/8 -5/4 13/4 \ край \ дясно) \ започне \ фантом \\ II \ cdot (-1) \\ \ фантом \ край \ стрелкаНадясно \ наляво (\ започне 1 -2 0 -5/2 5 -15 \\ 0 1 0 11/8 -11/4 15/4 \\ 0 0 1 5/8 -5/4 13/4 \ край \ дясно) \ започне I + 2 \ cdot II \\ \ фантом \\ \ фантом \ край \ стрелкаНадясно \\ \ стрелкаНадясно \ наляво (\ започне 1 0 0 1/4 -1/2 -15/2 \\ 0 1 0 11/8 -11/4 15/4 \\ 0 0 1 5/8 -5/4 13/4 \ край \ вдясно) $$
От последната от матрицата има общо решение на даден линейни системи: $ \ ляво \ x_1 = \ фракционатор \ fracx_4- \ fracx_5; \\ x_2 = \ фракционатор \ fracx_4 + \ fracx_5; \\ x_3 = \ фракционатор \ fracx_4 + \ fracx_5; \\ x_4 \ в R; \\ x_5 \ в Р. \ край \ прав. $. Основен разтвор се получава, ако свободните променливи се равняват на нула, т.е. $ X_4 = 0 $, $ x_5 = 0 $:
Продължение на тази тема, помислете за втората част. Нека разгледаме къде още два примера за намиране на общо решение.