WolframAlpha на руски как да разширят функциите в редовете на Фурие

Как да се разширява функцията в редовете на Фурие

Разширяването на функции в редовете на Фурие се използва доста често, тъй като в този си вид тя е удобно да се прави разлика, интегриране, използвайте компенсира аргумент на функцията, а намотка функции. Въпреки факта, че процедурата за разширяване на Фурие серия, дори и в най-простия случай може да отнеме доста време, системата Wolfram Alpha, като правило, лесно се справят с тази задача.

Представени в серия Фурие на тригонометрични и експоненциален (комплекс) форма:

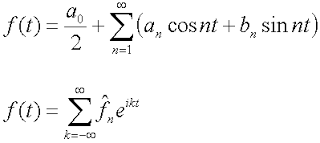
В първото изпълнение като система основа разлагане се използва Sines и уют. Но когато се работи с Фурие серия вместо това е по-удобно да се използва експонентата на един въображаем аргумент. Очевидно е така, Wolfram Alpha предпочита втория вариант.

Най-лесният начин за разширяване на функциите в редовете на Фурие - изпращане на заявка като серия Wolfram Alpha Фурие [функция аргумент, броят на гледна точка на серията]. Например,

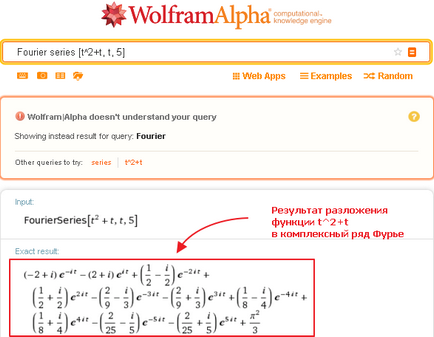
Получените резултати, както се изисква, представени в условията на разширяване на пета стаята включително; коефициентите на експонентата степени конюгатен комплекс спрегнати числа.

Едновременно Wolfram Alpha дава графично представяне на сближаване на серия дадена функция на Фурие (тук, централната част на графиката се доближава до предварително определено парабола):

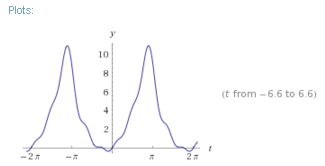
Още по-конкретно ясно Фурие приближение може да се види в резултатите от тази заявка (което се доближава права Фурие серия):

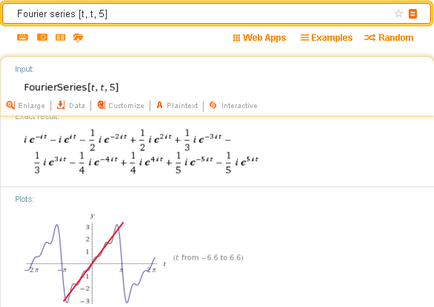
Въвеждане на дадена функция в редовете на Фурие на тригонометрични форма се показва в най-долната част на издаване (тук - за втория пример):

Между другото, въпреки факта, че по-горе проблем е системата: "Wolfram | Alpha не разбира вашата заявка Показване вместо резултат за заявка :. Фурие", - което означава "Системата не разбира вашата заявка показва резултатите, съответстващи на заявката: Фурие. "не се заблуждавайте от него;) при поискване" Фурие ", който предлага да се използва системата, ще бъде оттеглена или биографична информация за математик Жан-Батист Жозеф Фурие (математик). трансформация на функцията на Фурие [т ^ 2 + т] Фурие; в зависимост от това дали ще ви постави между думата "Фурие" и скобата на пропастта, или не.

Ако искането не посочва разширяване Фурие серия е ясно на броя на членовете на N, след това системата Wolfram Alpha по подразбиране показва четири варианта за п от 0 до 3, и само за комплекс под формата на Фурие серия:

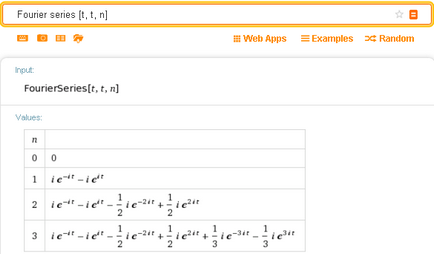
Допълнителни възможности за разширяване на п-голяма от 3 могат да бъдат получени веднага с помощта на "Още" бутона. Но това важи само за графичното представяне на резултатите:

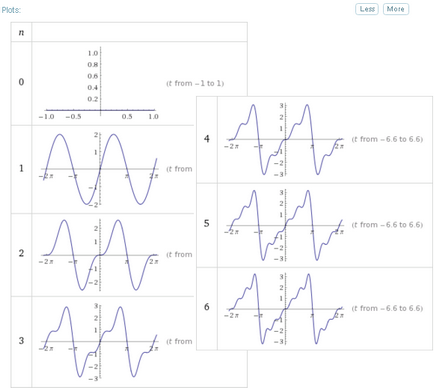
По този начин, за да се получи разлагането на функции в тригонометрични Фурие серия, е необходимо да направите заявка Фурие серия изрично посочва броя на термини в разширяването.

Какво да правим, ако задачата не е да се намери Фурие серия, коефициентите на Фурие серия?

На първо място, можете да използвате заявка FourierCoefficient [израз аргумент, п]. в която Wolfram Alpha система извежда п-ти коефициент разширяване експресия в комплекс серия Фурие.

Например, коефициентът на пети експресия разширение (т ^ 2 + т) в серия Фурие може да бъде получен както следва:

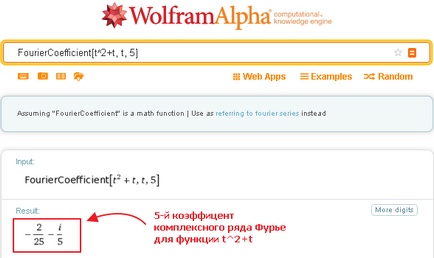
Ако, обаче, не се посочва изрично п, след заявката ще покаже общ израз за н-ти коефициента на Фурие серия от прояви на:

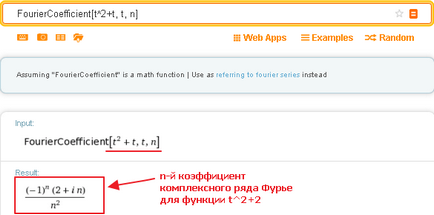
В допълнение, Wolfram Alpha след това показва една маса като поредица от сложни коефициенти на Фурие (до 15-ти мандат, включително, ако щракнете върху "Още"):

В този кратък преглед, аз не се споменава как да разширят функциите в редовете на Фурие на Синиш и уют, или как да използвате калкулатора за Фурие Systems Wolfram Alpha, и не каза нищо за двумерен Фурие серия. Всичко това - темата за бъдещите си постове. Следете блога.