Василий Василиевич Давидов

Илюстрация на компоненти на образователната дейност

Откъс от: VV Давидов

Сега, това е препоръчително да се даде конкретен пример за илюстрация на тези важни компоненти на учебна дейност, като задача обучение и учебни дейности, обща психологическа характеристика, която е дадена по-горе. Ние правим това на материал за изследване на деца от една от основните концепции на цялото училище математика - концепцията за номер 1 в клас.

Основната цел на този курс е до края на учениците от средните училища, за да се образува пълноправен концепция за реално число, което се основава на концепцията за стойност. Нашият курс започва с въвеждането на тази концепция се определя от отношението "е", "повече", "по-малко от". Ориентация към цялостните взаимоотношения позволява на детето да се извърши сравнение на разликата на тема представени стойности. Преди понятието асимилация може да записва резултатите от това сравнение се използват самите писмо формули като А = В; а> б; и

Въпреки това, в някои ситуации е трудно или дори невъзможно да се извърши директно сравнение на разликата и веднага се открие, например, равенство или неравенство на парични стойности (линии, товари и др.) Учителят демонстрира първокласници такива ситуации и про-седне им намери подходящ начин за решаване на проблема. Детски Различни хипотези и с помощта на учителите стигнали до извода, че в тези ситуации трябва да извършите косвени сравнения. Но какво е това? По какъв начин може да се направи? Как да работят с такива средства и какви резултати води? Учителят води децата на първия отчет на горните въпроси, а след това ги изправя пред ученето задача, изискваща откриването и усвояването на общия метод на непряко сравнение на разликата, въз основа на тяхното предварително пъти в сравнение с pomoschyuchisla.

Обучителните дейности, които позволяват да се реши този проблем, се фокусира върху търсенето, разкриване и разследване на имотите на деца, характеризиращи се с кратно на съотношението на количествата на записа е в модела просто показва броя на (по принцип - на действителния брой, въпреки че някои видове номера предполагат наличието на специални условия за изпълнението на множество връзки и изграждане на модела).

Първото действие обучение е да осиновят дете учи задачата, определена от преподавателя.

Когато вторият обучение деца действието упражнява такива обективни стойности трансформация, където множеството от връзки, намиращи се в тях. Детето открива някои трети стойност (Merck), с помощта на които е възможно да се определят началните стойности на двукратни изискваща диференциални сравнения. Например, стойностите на А и В не могат да бъдат сравнени директно (така че сегментите не може директно да се наслагват една върху друга). условия на проблема се превръщат дете, така че той намира някаква стойност C, използването на която ще му позволи да се определи колко пъти това количество C "форма" в стойностите на А и Б, тя позволява на детето да се определи тяхната съотношение пъти, което може да се запише с помощта на формули

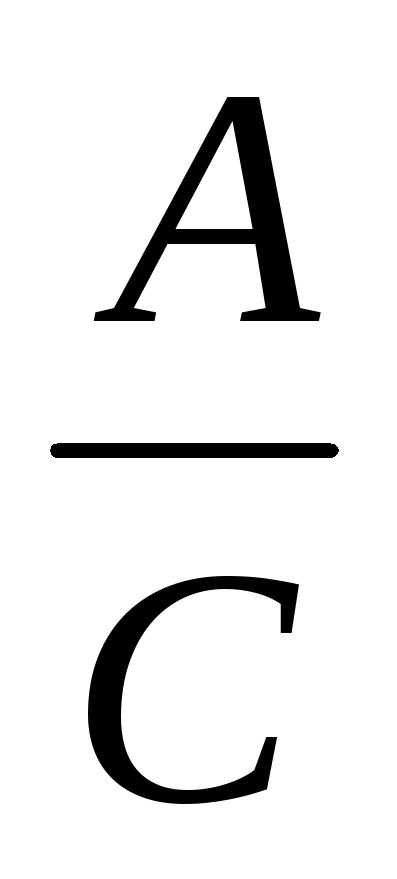
и 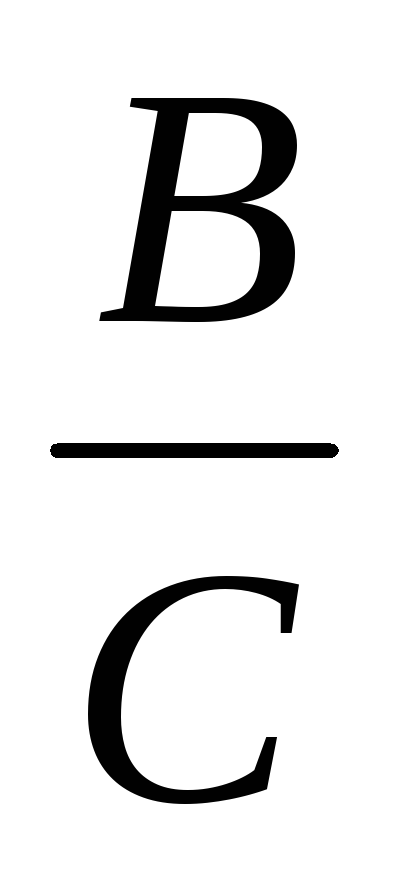(В бара означава множеството между букви).

Дейностите по трети обучение, свързани с моделиране на процеса на разпределяне на множество връзки и резултати. В този случай, симулацията се извършва от единството на обект, графични и писмо форми. По този начин, първоначално кратно съотношение може да се изрази с помощта на предмет или графични пръчки ( "етикети"), посочващи резултата като отделен "наслагване '' измервания, както и всички подобни" слоеве "(колко пъти това измерване се съдържа в най-големите чрез тяхното съотношение пъти) . след това, резултатите могат да бъдат представени в устна форма цифрите ( "един, два, три пъти ..."), след това с формула на множество отношения и медиирано съотношението разлика става:

В общи линии, тези формули могат да се напишат, както следва:

= К; K <М; А <В.

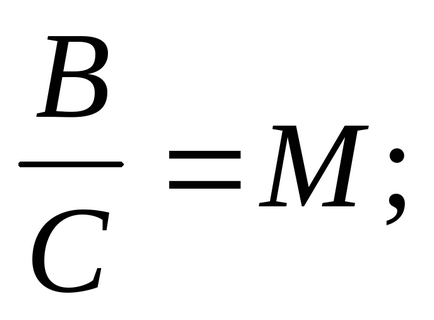
По този начин, буквално модел на процеса и в резултат на избор на множество взаимоотношения в общи линии е както следва:

= Н. В тази обща формула може да се изолира и деца fiksirovatlyuboe прегъване стойности съотношение, изразено в съответния специфичен брой (например, данни А и С е представен чрез съотношението на броя 4). От съотношението на самите тези числа (т.е., броят на свойства като модел на множествена връзка) могат да бъдат медиирани от решаване на проблема с първоначалното сравнения разликата.

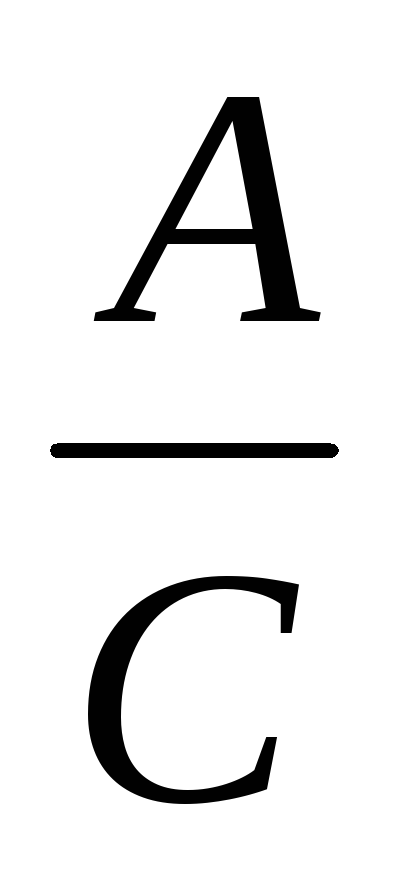
Четвърто образователна действие се състои в трансформация на модела, избран съотношението, което ни позволява да учат своите общи свойства. Така, С Измерванията се променят в същото първоначална стойност А води до промяна в определен брой, показваща връзката им. Ето защо, например, ако

= К и

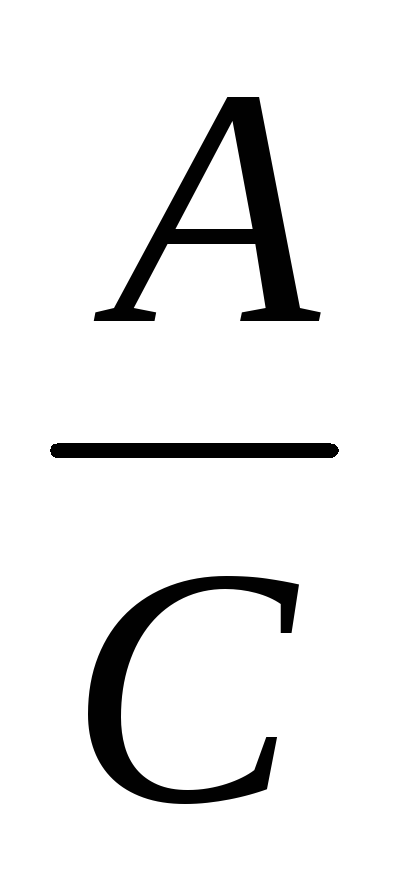
Най- <С, то

> К и т.н.

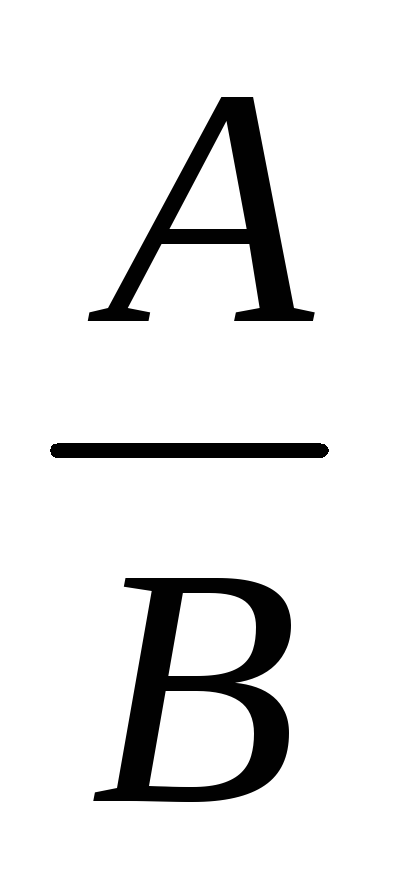
Усвояването на децата съдържанието и последствията от действията на обучение е от съществено значение в запознанството им със света на номера и се превръщат в характеристика на решението е образователен проблем, когато някои от най-често срещаните свойства на номера се учи децата да се запознаят с разнообразието от конкретните им проявления.

Пето спецификация действие обучение се отнася до общия метод на откриване на множество отношения и решения конкретни задачи включва установяване и определяне на специфични номера характеризиращи връзката е доста някои променливи (например, намирането на цифровата характеристика на конкретен непрекъснати или дискретни стойности на дадена мярка). Това действие позволява на децата да се отнасят на общия принцип за получаване на броя на частичните набори условия soschityvaniya или непрекъснато измерване на обекти. В този случай, по-вярно разбиране на броя търси във факта, че детето може да се движи свободно от една мярка в друга при определянето на числени характеристики на един и същ обект, и по този начин се съпоставят със себе си различни конкретни числа (една и съща стойност може да се съпостави с разнообразие от конкретни числа ).

По този начин, първоначално обучение на деца да решат проблема чрез изграждане на общ метод за получаване и едновременно с това да поемат своята концепция. Сега те могат да използват този метод и съответната концепция в най-различни ситуации, които изискват числено описание на обектите.

Друго обучение ефект - контрол позволява на децата при запазване на общата форма и смисъла на предходните четири действия за промяна на тяхната оперативна структура, в зависимост от конкретните условия на прилагането им, специфичните характеристики на материала (поради това действие са умения inavykami). Екшън navseh етапи за оценка на студентите решения учебни задачи цели на другите си дейности за обучение на крайния резултат - получаване и използване на номера като специални средства за съвпадение стойности.

Ние очерта накратко тези учебни дейности, които позволяват на децата да се научат на концепцията за базирани на съдържание (теоретично) обобщение. В процеса на обучение в реално тези действия, разбира се, имат по-сложна структура, разкриването на която предполага по-подробно описание на дейности за обучение по математика на класната стая.