Състояние перпендикулярна вектор

В тази статия, ние ще обърне специално внимание на състоянието на две перпендикулярни вектори в равнината и в триизмерното пространство, както и намирането на координатите на вектора, перпендикулярни една двойка или група от вектори. Тази тема е важна, защото има значителен брой проблеми (например, на предизвикателствата, свързани с уравненията на линии и равнини), решаването на които се основава на констатацията на вектори перпендикулярна на известни вектори.

На първо място, ние ще се справим с необходимо и достатъчно условие за две перпендикулярни вектори. След това, от състоянието на перпендикулярност ние получаваме метод вектор констатация даден вектор, перпендикулярна на равнината, в пространството. В заключение, нека разгледаме един начин за намиране на вектор, перпендикулярна на двете два вектора. Не забравяйте да дадете някои подробни решения на примера.

Навигация в страниците.

Необходимо и достатъчно условие за две перпендикулярни вектори.

Припомнете определението на ортогонални вектори в равнината и в триизмерното пространство.

Две ненулеви вектори се наричат ​​перпендикулярно. ако ъгълът между тях е равно на деветдесет градуса (радиана).

Какво мисли предлагам това определение, когато трябва да знаете две перпендикулярни векторно изображение, или не?

Ако някои точка на самолета да забави равни вектори дадени вектори, след това с помощта на транспортир може да се измери между тях ъгъл. Това позволява известна степен на точност вектори перпендикулярността (ако са получени деветдесет градуса ъгъл, когато се измерва). В този случай, разбира се, трябва да се вземат под внимание точността на строителството и точността на измерване. Такъв метод за определяне на хоризонталността на два вектора трябва да се използва само, когато ние не знаем нищо за тези вектори, а има само имиджа си в самолета.

На практика често се окаже да има две ненулеви вектори перпендикулярност, когато са известни със своите координати в правоъгълни координатна система в равнината или в пространството. В този случай, необходимо и достатъчно условие за две перпендикулярни вектори. Ние го посочи като теорема.

За хоризонталността на две ненулеви вектори и е необходимо и достатъчно условие е скаларен продукт е равно на нула, т.е., че равенството.

Да предположим, че векторите и са перпендикулярни. Нека докажем равенството.

От дефиницията на скаларното произведение на векторите е равна на произведението на техните дължини от косинуса на ъгъла между тях. Тъй като векторите са перпендикулярни, ъгълът между тях е равно на деветдесет градуса, следователно, както се изисква.

Ние се обръщаме към втората част на доказателството.

Сега ние мислим. Ще докажем, че векторите и са перпендикулярни.

Тъй като вектори и не-нула, от факта, че. Така косинуса на ъгъла между вектори е равна на нула и, следователно, ъгълът е равен, което показва, че векторите и перпендикулярността.

Следователно, необходимо и достатъчно условие за две перпендикулярни вектори се доказва.

Тъй като условието изглежда хоризонталността на два вектора в компонент форма?

В скаларен продукт координатите Ние показахме, че два вектора с дадени координати и равнина половете, и за двата вектора в пространството. Следователно, необходимо и достатъчно условие за перпендикулярност на двата вектора в координати е в равнина, и триизмерното пространство.

Помислете за прилагането на тези условия на практика, това решение се анализират няколко примера.

дали векторите са перпендикулярни.

От състоянието на перпендикулярни вектори имаме. Нека допуснем, а след това, идва от. Така, векторът - един от векторите, които са перпендикулярни на вектора.

.

Подобно търсене вектор, перпендикулярна на даден вектор в триизмерното пространство.

За вектор има безкрайно множество от ортогонални вектори. Ще покажем това. Нека вектора се намира на линията А. Ние означаваме с произволна равнина, перпендикулярна на права линия а. Тогава всеки ненулев вектор, принадлежащо към равнина, перпендикулярна на вектора.

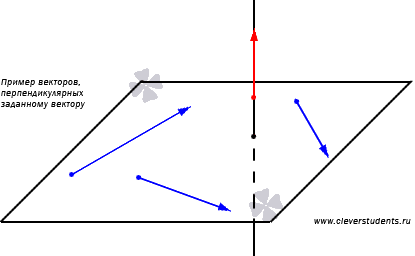
Ние показваме как да се използват условията на перпендикулярността вектори са координатите на вектор, перпендикулярна на даден ненулев вектор.

Нека вектора има координатите и. Намерете ги.

От състоянието на две перпендикулярни вектори на равенството. Тъй като векторът е нула, тогава поне един от нейните координати е различна от нула. Нека (или можете да вземете). След това тя може да бъде разделена на координатната от двете страни, като в същото време се получи. По този начин, като координатите и произволни стойности, поне една от които е различна от нула, и изчисляване по формулата, получаваме вектор перпендикулярен на даден вектор.

Нека разгледаме следния пример.

Намерете координатите на вектор перпендикулярен на вектора.