Сила на Лоренц - studopediya

Магнитното поле на движещ се заряд

- сила, упражнявана от магнитното поле на електрически зареден движещ на частиците.

където Q - зареждане на частицата;






V - скорост на таксата;
Б - магнитна индукция;
а - ъгъл между скоростта на заряда и на вектора на магнитната индукция.

Лоренц посока сила се определя от правилото на лявата ръка:

Ако поставите лявата си ръка, така че перпендикулярно компонента на вектора на скоростта на индукцията е бил част от дланта и четири пръста трябва да бъдат разположени по посока на скоростта на движение на положителен заряд (или срещу посоката на скоростта на отрицателен заряд), наведе палец посочи посоката на силата на Лоренц

.

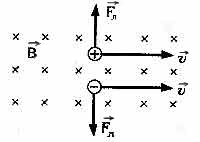
Тъй като сила на Лоренц е винаги перпендикулярна на скоростта на зареждане, тя не работи (т.е. не променя размера на скоростта такса и нейната кинетична енергия).

Ако една заредена частица се движи успоредно на магнитните силови линии, на ет = 0 и такса в магнитно поле и dvizhetsyaravnomerno праволинейно.

Ако една заредена частица се движи перпендикулярно на магнитните силови линии, в сила на Лоренц е центростремителна

и създава центростремителна ускорение равно

В този случай, частицата се движи в кръг.

.

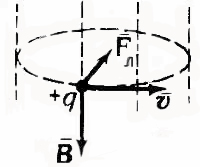
Според втория закон на Нютон: Лоренц сила ravnv продукт на масата на частиците в центростремителна ускорението

тогава радиусът на кръга

и периода на завъртане на заряд в магнитно поле

Тъй като електрическият ток е наредено движение на обвиненията, ефектът от магнитното поле на тоководещи проводници, е резултат от влиянието си върху отделни движещи се заряди.

Ако направите токопровеждащите проводник в магнитно поле (fig.96, а), виждаме, че в резултат на добавянето на магнитните полета на магнита и диригент ще засили в резултат на магнитното поле от едната страна на проводник (в горната част на фигурата) и отслабването на магнитното поле от другата страна проводник (на чертежа по-долу). В резултат на двете магнитни полета ще кривина на магнитните линии и те се опитват да намалят, ще изтласка през проводник (фиг. 96 б).

Посоката на силата, действаща по текущата балансова проводник в магнитно поле може да се определя от "правило лява". Ако лявата ръка разположен в магнитно поле, така че магнитните силови линии, които произхождат от северния полюс, така да се каже в дланта и четири пръста разширени съвпада с посоката на тока в проводника, големите ръце сгънати пръста ще показват посоката на силата. Ампер сила. в качеството на дължината на елемента на проводник зависи от магнитната индукция B в проводник текущата стойност на I, дължината на елемента на проводник и синуса на ъгъла а между посоката на дължината на елемента на проводник и посоката на магнитно поле. Тази връзка може да се изрази с формулата:

За линеен проводник ограничен дължина поставя перпендикулярно на постоянно магнитно поле, силата, действаща върху проводника, ще бъде равен на:

От последното уравнение ние определяме размера на магнитната индукция.

Тъй като измерение на властта

т. е. на размера на индукцията на един и същи вид е било получено от нас от закона на Био и Савар.

Тесла (единица на магнитната индукция)

Тесла, магнитната индукция единица Международната система единици, която е равна на магнитната индукция, в който магнитния поток през областта на 1 м 2 напречно сечение е 1 до Weber. Тя носи името на Tesla. Легенда: Руски въшка, международна Т. 1 тесла = 104 гауса (гауса).

Магнитната момента. магнитен диполен момент - основната количество характеризиране на магнитните свойства на материала. Магнитния момент се измерва в # 8901; m 2 или J / T (SI) или ерг / Гаус (GHS), 1 ерг / гауса = 10 -3 J / T. Специфична елементарна единица на магнитния момент е Бор магнетон. В случай на равен контур с електрически ток магнитния момент се изчислява като

,

при което - тока във веригата, - зоната на контур, - единица вектор нормална към равнината на линия. Посоката на магнитния момент обикновено е по правило дясно: ако завъртане палец копчето в посоката на тока, посоката на магнитния момент ще съвпадне с посоката на движение напред на палеца.

За всеки затворен контур на магнитния момент е:

,

при което - радиус вектор от произхода на елемент верига на дължина

В най-общия случай на разпределението на тока в среда:

,

където - плътност на тока в елемент обем.

Така че, със сегашната линия на магнитното поле оказва въртящ момент. Circuit ориентирана поле в даден момент само по един начин. Предполагаме, за положителната посока на нормалната посока на магнитното поле в този момент. Въртящият момент е пряко пропорционална на ток I. контур площ S и синуса на ъгъла между магнитното поле и нормалната.

тук M - въртящ момент. или въртящ момент. - магнитен момент на цикъла (подобно - електрическа диполен момент).

неравномерно поле () формула е валидна, ако размерът на схема е малък (когато може да се счита веригата в областта приблизително еднакво). Вследствие на веригата с ток все още има тенденция да се обърнеш, така че неговата магнитен момент е насочен по посока на векторни линии.

Но освен това, контура на получените сила действа (в случая на еднородно поле, и. Тази сила актове на пистата с ток или въртящ момент от постоянен магнит и ги въвлича в района на силно магнитно поле.
Работата по пътя на изместване с ток в магнитно поле.

Лесно е да се докаже, че работата по веригата с ток движещ се в магнитно поле е равна. и където - магнитни потоци през зоната на контур на крайните и началните позиции. Тази формула е валидна, ако токът във веригата е постоянна. т.е. при преместване на веригата не е взето предвид явлението електромагнитна индукция.

Формулата е валидна за големи вериги в силно нехомогенни магнитно поле (приемайки, I = CONST).

И накрая, ако текущата контура да не измести и промяна на магнитното поле, т.е. промяна на магнитния поток през повърхността заобикалящата контура на стойност към него за тази цел е необходимо да се извършват една и съща работа. Тази работа се нарича промяна на работата в магнитния поток, свързан с веригата. Поток на магнитната индукция (магнитен поток) чрез DS този район се нарича скаларна физическо количество, което е равно на

където Вп = Vcos # 945; - проекция на вектора в посока перпендикулярна на DS повърхностните (# 945 - ъгълът между вектори п и В), DS = DSn - векторни чийто модул е ​​равен на DS, и неговата посока съвпада с посоката на нормалната п към сайта. Векторът поток може да бъде или положителен или отрицателен в зависимост от знака на COS # 945; (Предвид от избора на положителната посока на нормалната N). Векторът поток обикновено е свързана с веригата, чрез които протича ток. В този случай, е било указано положителната посока на нормалата на контура на контакта: тя е свързана с текущите правила на десния винт. Следователно, магнитния поток, който се създава контур през повърхността, ограничена от себе си, е винаги положителен.

А магнитен поток чрез произволно вектор FB целевата повърхност S е равна на

За равномерно поле и плоска повърхност, която е перпендикулярна на вектор В. Вп = В = конст AND

От тази формула дадена единица Weber магнитен поток (Wb) 1 Wb - магнитен поток, който преминава през зоната на планарна повърхност на 1 м 2, която е перпендикулярна на постоянно магнитно поле и индукцията е равно на 1 тесла (1 тесла = 1 Wb • m 2) ,

теорема Гаус "на поле вектор Б. поток на магнитната индукция чрез всяка затворена повърхност е нула:

Тази теорема е отражение на факта, че не са налице магнитни заряди. при което магнитния поток линии няма начало и край и са затворени.

Следователно, векторите за потоци В и Е чрез затворена повърхност в вихър и потенциални области, получени от различни формули.

Като пример, ние откриваме поток вектор B чрез соленоид. Магнитна индукция равномерно поле в магнитната бобина със сърцевина с магнитна проницаемост # 956;, равен

Магнитният поток чрез намотка на соленоида е равна на площта S

и общата магнитния поток, който е свързан с всички електромагнитни бобини и наречен поток,