Редовни цифри и тяло - studopediya
"Питагор трансформира геометрия, което му придава формата на свободна наука, за това, което принципи чисто абстрактен начин и проучване на теоремата с нематериален и интелектуална гледна точка. Той беше този, който намери теорията на ирационални числа и структура на небесни тела. " Така ценен принос за Питагоровата геометрия Прокъл и тази оценка древен философ с право.
В действителност, училище Питагоровата геометрия в независима научна дисциплина. Това беше Питагор и неговите последователи са първите, които систематично изучаване на геометрията - като теоретична доктрина от свойствата на абстрактни геометрични фигури, а не като колекция от рецепти, прилагани от геодезически измервания. В този случай, най-важното е, че свойствата на геометрични фигури Питагоровата които не са установени чрез измерване при използване на логически доказателства.
С най-широк областта на практическо приложение, геометрията на първите учения на Питагоровата # 956; # 940; # 952; # 951; # 956; # 945; Той хвърли було на "тайна" и се превърна в най-популярната наука. Въпреки това, в "Животът на Питагор" причини за популярността на геометрията представи малко по-различно Iamblichus: "Това е начина, питагорейците обяснят защо геометрия става достъпен за обществеността. Това беше по вина на един от тях, който е загубил пари питагорейските общности. След тази катастрофа общност му позволява да печелят пари с помощта на геометрията - геометрията се нарича "питагорова Традиция". Като се има предвид, че V инча Преди новата ера. д. Те са били много популярни софисти - пътуващ учител на мъдростта, това е напълно възможно, че питагорейците не се колебайте да се запълни хазната на преподаване.
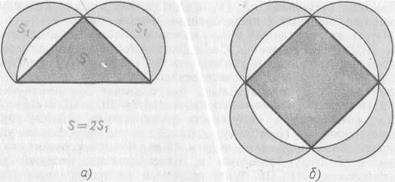
По този начин, благодарение на Хипократ от Хиос, имаме основание да се смята, че питагорейците като цяло са построили цял планиметрия праволинейни форми. Те са изучавали свойствата на триъгълници, правоъгълници, успоредници, трапецовидна доказа теоремата за сумата от ъглите на триъгълника, теоремата на страната на триъгълника, който се намира срещу тъпият ъгъл, за равенство на теоремата на триъгълници. Пикът на геометрията на самолет на праволинейни фигури е доказателство на известната теорема на Питагор. Тези резултати Питагоровата геометрия, очевидно, и формира основата на книгата "елементи" на Евклид, която завършва Питагоровата теорема.
Питагорейците показват повишен интерес към правилните фигури и органи. Редовните геометрични форми, дължащи се на "правилно", т.е.. Е. присъствието или въртящ огледалото (и често една или друга) на симетрия, както и възможно по цялата Питагоровата отговори на редовен, структурно подредени хармонична структура на вселената. (Този въпрос ще се върнем към по номера. 2.2 и 4.3.) Геометрична форма, особено на правото, най-впечатляващо разкри броя и не може да бъде по-подходящ за "извличане на няколко неща." Питагоровата положи един от другите геометрични форми (обикновено в дясно или "носител" някакви "свещени" номера) и в този, наблюдаван постигане на съгласуваност явления.
Ето защо питагорейците прикрепени особено значение, за да ги доказва теорема, че самолет може да бъде напълно (т.е. няма "дупки" и наслоявания ..) за покриване само три редовни полигони: триъгълници, квадрати и шестоъгълници (Фигура 42.). Доказателството на теоремата е доста прозрачна, а ние да го оставя на читателя. Не е трудно и изграждането на правилни фигури, а цифрите, получени от тях чрез удвояване на двете страни.

Но сега изграждането на равностранен петоъгълник вече не е толкова очевидно. Ние не знаем как да се построи равностранен петоъгълник питагорейците. Но е известно, че на петолъчна звезда - неговата основна символ и знак за маркировка - те се състоят от три равнобедрени триъгълници. Това ясно повтаря метода за изграждане на редовен петоъгълник, описан от Евклид ( "елементи", Vol. IV на, предишна. 11). Така че методът на Евклид, вероятно датира от питагорейците. Помислете за това.
Като се има предвид кръг вписан в равнобедрен триъгълник ACD. кой. (Метод за изграждане такъв триъгълник ние посочи в сек. 2.2.) И начертайте ъглополовяща CE DB ъгли В и Г. След това ъглите на 1-5. (Фигура 43) са равни, и следователно, ще бъде равна на съответната дъга и затягането на хордата, т.е., ... Така че, вписан в ABCDE на кръга е равностранен петоъгълник. Тъй като и двете ъглите, на базата на една и съща дъгата AB и AE, съответно, всички ъгли 1 - 7 са равни и следователно всеки ъгъл на петоъгълник ABCDE ще се състои от три равни ъгли, т.е., ... Така конструирана петоъгълник е равностранен и равни ъгли, т. Е. бъде.
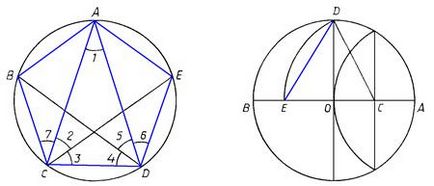
С течение на времето, гръцкият математик беше установено по-лесен начин да се построи равностранен петоъгълник. Той е описан в друг изключителен състав древността - "Almagest" Птолемей (около 150.), която, подобно на "началото" на евклидовата геометрия, енциклопедия на древните познания по астрономия. Птолемей разделя наполовина радиус кръг ОА (С точка) и CD описва радиус кръг до пресечната точка с диаметър AB в точка Д (фиг. 44). Тогава ED е на страната на равностранен петоъгълник. (След като прочете параграфа. 2.2 Читателят може лесно да го докажа себе си.)
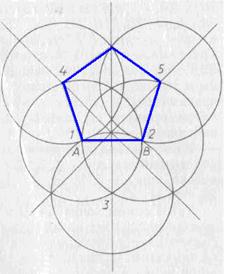
След още хилядолетие и половина, през 1525 Albreht Dyurer (1471-1528), художник и учен, един от титаните на Възраждането, в своя трактат "Ръководство за измерване с помощта на владетел и компас" имат приблизителен метод за изграждане на равностранен петоъгълник от дадена страна AB с с помощта на "ръждиви" компаси, т. е. един разтвор шублер. Метод Dürer ясно от фигура 45, където цифри обкръжават крака са последователно идентифицирани. метод Dürer различава висока точност (ъгли 1 и 2 не са равни на 108 °, а. Ъгли 4 и 5, малко по-голям от 107 °, докато ъгъл С малко повече от 109 °), така че нейните грешки в окото не е напълно възприемат. Самият Дюрер не се споменава за приблизителния характер на техните конструкции, може би ги има предвид, че са точни. Независимо от това, методът на Дюрер е приблизителна. (Опитайте се да го докаже.)
И как да се изгради с помощта на линийка и компаса след правилната фигура - Седмоъгълник? Тази задача е обезсърчително не само древните питагорейците, но остава нерешен повече от две хилядолетия! Само през 1796 г., 19-годишният немски момче Карл Фридрих Гаус (1777-1855), по прякор Царя късно математици го решават. Гаус е показано, че проблемът за изграждане на началник и компас правилен N-ъгълник, е еквивалентно на проблема за разделяне на окръжността в п равни части, тя е свързана с корените на изследването. Освен това, Гаус доказва, че редовното N-Гон може да бъде изградена от владетел и компас единствено и само ако N - председател на формата
Prime номера на формата (2.1.1) са посочени броя на стопанствата, и все още знаят само пет от тези номера :.
Това Gaussian резултат обобщава в случая, когато броят на страните на многоъгълник п е продукт на номера на формата (2.1.1). Като се има предвид също така възможност за удвояване н. Ние се формулира Гаус теорема. правилен многоъгълник може да се строи с помощта на компаса и владетел, ако и само ако броят на страните му има формата
В действителност. тъй като други числа на Ферма е все още неизвестен.
Лесно е да се види, че всички полигони, които са били в състояние да изгради на древните гърци, а именно тези, които имат. съдържащ се в (2.1.2). По този начин, чрез добавяне на нови антични многоъгълници с п = 17, 34, 51, 68, 85, 126, 252, 255, и 257. Новият принципа на това са 17-гон-гон 257 и 65 537 гон. Гаус откри метод за изграждане на първите две от полигоните. Имайте предвид, че описанието на метода на изграждане на 257-гон Гаус отне около петдесет страници. Гаус живот е изключително горд от младостта си откритие и завещал гравирани върху надгробния му камък редовен 17-Гон вписан в окръжност.
Така правилен многоъгълник конструиране началник и компас възможно, когато п = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, .... не може, когато п = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33.
Сега се обръщаме към редовната polyhedra. Има само пет, а Прокъл освен забележителните открития в планиметрия приписва на Питагор изграждането на петте редовни твърди вещества. Днес, обаче, математици, историци предпочитат да не вярват прокълнат, и е установено, scholium (# 963; # 967; # 972; # 955; # 953; # 959; # 957; - тълкуване, обяснение) в XIII книгата "Елементи" на Евклид, където се казва, Питагор е знаел само три правилния орган - тетраедър, шестостен (куб) и додекаедър, а по-късно отвори Theaetetus, а останалите две - октаедъра и icosahedron. В този и в друг случай, древната доказателствата ни кажете за интереса на питагорейците към правилните органи.
Изглежда, че самата природа предизвика питагорейците под формата на обикновен телефон: солни кристали имат форма на куб, стипца - октаедър и кристали от пирит - додекаедър. На последно място, както се вижда от разкопките в Италия, е бил любимо деца играчка etbolgarskih във времето на Питагор.
Името на регулярна полихедронов се определя от броя на ръбовете му (например тетраедър - # 964; # 949; # 964; # 961; # 940 - # 949; # 948; # 961; # 959; # 957; - # 964; # 949; # 964; # 961; # 940; # 962; - chetype + # 949; # 963; # 961; # 945; - област на тялото, лицето - тетраедър). Редовните polyhedra са показани на фигура 46 и техните геометрични характеристики са обобщени в таблица, където m означава броят на лицата на върха.
Питагорейците забелязали, че куба на броя на върховете (8) е хармонична средна стойност на броя на повърхности (6) и брой ребра (12) и следователно се нарича кубичната хармонична тялото. куб специална мисия е наблюдавано и в това, че той е бил само на редовни твърди напълно запълва пространството.
По време на Евклид, беше отбелязано, че куб и октаедър, додекаедър и icosahedron са двойно (двойно), т. Е. Броят на повърхности на тялото, равен на броя на върховете на другия и обратно. След това, едно тяло може да бъде получена от друг, ако центровете на лицата да приемат върховете на друга, или обратно (фиг. 46). Tetrahedron е двойна към себе си.
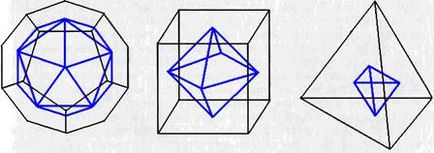
Все пак, най-важното свойство на изпъкнал polyhedra е установено само в средата на ХVIII век. Теорема на Ойлер. в произволен брой върхове на изпъкнал многостен (L) плюс броя на лицата (М) минус броя на перките (N) е с постоянна стойност, равна на две:
И все пак най-интригуващата характеристика на редовни твърди частици е, че те съществуват само пет. Не случайно доказателство за този факт е завършена последните XIII книгата "Елементи" на Евклид. [44] В действителност, количеството на равнина S в ъглите връх на изпъкнал многостен трябва да бъде стриктно по-малко от 360 °, докато броят на лицата на върха. Така че, пред които е изправена редовни твърди частици могат да бъдат само три редовни полигони: триъгълник, квадрат, петоъгълник, шестоъгълник, защото дори и за. можете да направите три правилния орган на равностранен триъгълник: - тетраедър - октаедър и - един icosahedron (с). От площади и редовни петоъгълници - само един (куб и додекаедър), когато (ако - за квадратите и - за петоъгълници). По този начин, редовен polyhedra може да бъде само пет.
Този факт не може да остане безразличен склонни към числен мистицизъм на питагорейците, а зад тях, Платон и неоплатонисти. Платон разработен известната доктрина на петте "елементи" - основа на Вселената, атомите на които тя е замислена под формата на редовни твърди частици. (Повече Plato това учение ще бъде обсъдено в т. 4.3). От тогава, редовни многостени често се нарича платоническите твърди вещества.
Редовен polyhedra в цялата история на човечеството не престава да се полюбувате на симетрията на питане ум, мъдрост и съвършенство на своите форми. Леонардо да Винчи обичаше бърникането скелети редовни твърди частици и да ги представи като подарък аристокрацията, може би в опит да се приложи правомощията, които се към философски размисъл върху красотата на вечните истини (фиг. 47).

Фиг. 47. Чертежи на дървени модели на додекаедър и icosahedron, направени от Леонардо да Винчи за книга на приятеля си Лука Пачоли "На Божествената Пропорция." Венеция. 1509
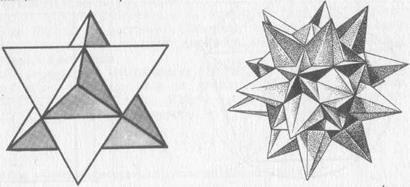
Фиг. 48. Фиг. 49. седми звездообразна Архимед тялото - icosidodecahedron.