Подготовка на учениците за изпита и OGE (ДПА) в резолюцията на център за обучение (наръчник по математика -

трансформира самолет

Определение 1. Преобразуването на равнината се нарича правило. от които всяка точка на равнината има съответства точка на една и съща равнина.

Определението на 1 означава, че ако F - трансформация на равнина алфа на. и М - произволна точка на самолета. на F (М) е точка на равнината на алфа.

2. Определяне на точка F (M) се нарича точка на изображението М при конвертиране точка М F. прототип, наречен F (М) в точката на конвертиране F.

Се определят по подобен начин и обратни изображения на всички части на самолета на трансформация F.

3. Определяне на трансформация самолет нарича себе си биективен трансформация самолет. ако различни точки имат различни изображения. и всяка точка е обратен изображение равнина.

С други думи, когато едно към едно преобразуване на самолета на различни точки от равнината се премести в различни части на една и съща равнина, както и във всяка точка на самолета минава някакъв момент на този самолет.

ОПРЕДЕЛЕНИЕ 4. продукт (състав) на две трансформации се нарича трансформация, която се получава чрез последователно провеждане на тези трансформации.

По този начин, ако F и G - две реализации, продуктът на тези трансформации ще бъде трансформация от Н, А е произволна точка в равнина, трябва да се отбележи А "на тази равнина, определена от формулата:

равнината на движение

ОПРЕДЕЛЕНИЕ 5. Движение равнина се нарича равнина трансформация, в която разстоянието между две точки в равнината е равна на разстоянието между техните образи.

Следните трансформации са равнинни движения:

1. паралелно предаване (изместване) на предварително определено вектор

Успоредно транспортен самолет с предварително определен вектор (Фиг.1) равнината на произволна точка преминава в точка А равнина ", както равенството

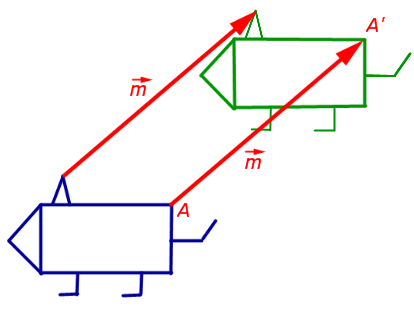
Забележка. Движение, в която всяка точка на равнината остава на място, наречено трансформация на идентичност. Трансформацията на идентичност може да се разглежда като паралелен превод на вектор, равна на нула.

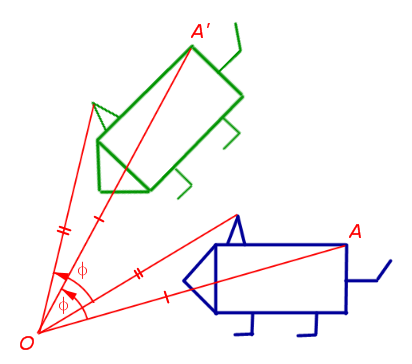
2. въртене около определен момент наречен центъра на въртене на предварително определен ъгъл

Чрез завъртане на равнината около точка O от φ ъгъл (фиг. 2) да бъде произволна точка А в равнината преминава равнина точка А ', че равенства

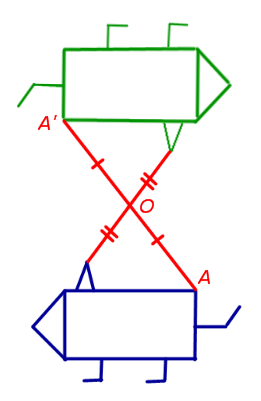
3. централната симетрия (симетрия по отношение на предварително определена точка, наречена център на симетрия)

В централната равнина на симетрия по отношение на точка O бъде произволна точка А в равнината минава точка А "равнина като средата на АА сегмент" е точка О - предварително определена симетрия център (Фигура 3).

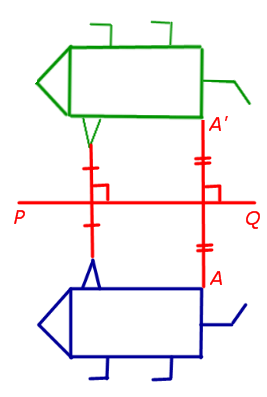
4. аксиална симетрия (симетрия по отношение на дадена линия, наречена оста на симетрия)

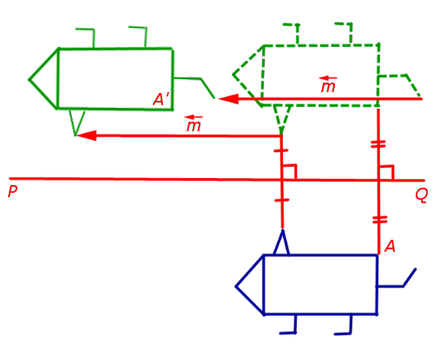
Когато аксиална симетрия по отношение на права линия PQ (ос на симетрия) на на произволна точка А в равнината минава точка А "равнина, че, от една страна, линията АА ', перпендикулярна на линията PQ. и второ, точката на пресичане на АА линии "и PQ е средата на АА '

5. Плъзгащ симетрия (състав аксиална симетрия по отношение на дадена линия и паралелно прехвърляне на предварително определен ненулев вектор успоредна на тази права линия)

Ако линията PQ - симетрия ос и вектор паралелно превод се дава чрез паралелна линия PQ. преместване резултат на симетрия може да бъде конвенционално представена както следва, както е показано на фигура 5.

Предложение ориентация равнина запазване. Предложение самолет промяна на ориентацията. теорема Sala

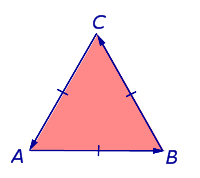
Помислете за произволна равнина равностранен триъгълник, а буквите означават върховете А, Б и В, така че да става по страните на триъгълника в посока

триъгълник са разположени отляво (Фиг.6). С тази нотация върховете на обиколка триъгълник ще се извършват на часовниковата стрелка.

Да предположим сега, че някои движение F отнема триъгълника ABC в A'B'C триъгълник ", който

Тъй като всяко движение на самолета запазва разстоянието между точките, триъгълника A'B'C "също ще равностранен, обаче, в следните два случая.

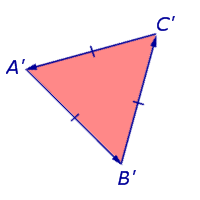
В първия случай, байпаса на страните на триъгълник A'B'C "в посока

Триъгълник A'B'C се намира в ляво. и байпас се извършва обратна на часовниковата стрелка (Фигура 7).

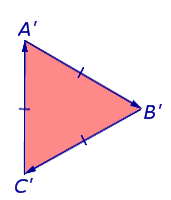
Във втория случай, една верига заедно от двете страни на триъгълник A'B'C "посока

Триъгълник A'B'C се намира в дясно. и байпас се извършва в посока на часовниковата стрелка (Фигура 8).

Дефиниция 6. Ако първия случай се реализира, когато се движат F, то това движение е движението, който запазва ориентацията на самолет (движението на първото вид, правилното движение). Когато F движение се извършва втория случай, това движение се нарича движение, промяна на ориентацията (движение на 2-ри вид, неправилно движение).

Класификация на всички движения на самолета дава следната теорема Сала.

Chasles теорема. Всяко ориентация движение равнина запазване, или паралелно изместване. или завъртане. Всяко равнинно движение промяна ориентация, е или аксиална симетрия. или отражение плъзгане.

Affine трансформация равнина

7. Определяне на афинно преобразуване равнина се нарича самата трансформация равнина един към един, където всеки директен начин на самолета е права линия.

Тъй като всяка равнина движение носи прави линии в прави линии, всяко движение е трансформация афинно.

Въпреки това, афинни трансформации не се ограничават до равнината на движение. Следните трансформации са също афинно преобразуване равнина:

1. компресиране (разтягане) на линията с коефициент на предварително определен компресия (разширяване)

По време на компресия (разрастване) на равнината на правата линия PQ зададени компресия к (Фиг.9) равнината на произволна точка преминава в точка А равнина ", които са изпълнени следните условия:

• Директен AA ', перпендикулярна на линията PQ;
• ако е маркиран с буквата А "пресечната точка на АА линии" и PQ. няма да има равенство

| Ã'â "| = | к | | АА" | ;

ако к> 0. След това точките А и лъжата А "от едната страна на PQ на линия. ако к <0. то точки A и A' лежат по разные стороны от прямой PQ .

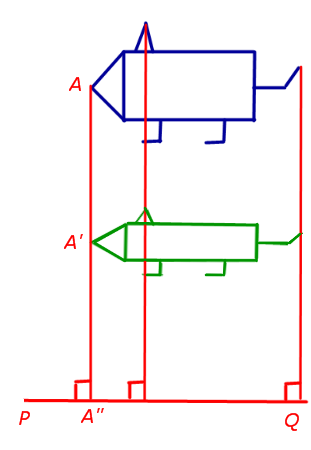
Забележка 1. В случаите, когато | к | <1. рассматриваемое аффинное преобразование называют сжатием к прямой PQ. если же | k |> 1. че тази трансформация се нарича дилатация.

Забележка 2. Ние ще използваме за дадената компресията (напрежение) обозначение

2. компресия (опън) от две предварително определени взаимно перпендикулярни посоки с предварително определен коефициент на компресия (разширяване)

Нека PQ и MN - две взаимно перпендикулярни прави линии и номера К1 и К2 - съотношения на компресия (удължаване) равнина в посока на линии PQ и MN, съответно. Тогава компресия (разширяване) в две взаимно перпендикулярни посоки уточни PQ и MN с коефициенти k1 и k2 (Фиг.10) се нарича компресии състав (разтегля).

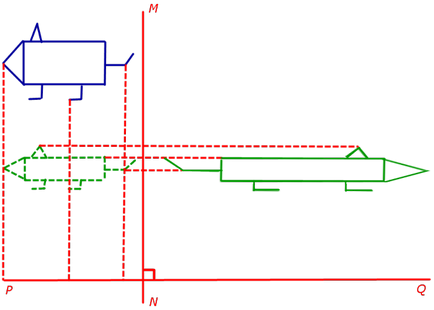
3. хомотетно трансформация с предварително хомотетно център и зададени степента на сгъстяване (разширяване)

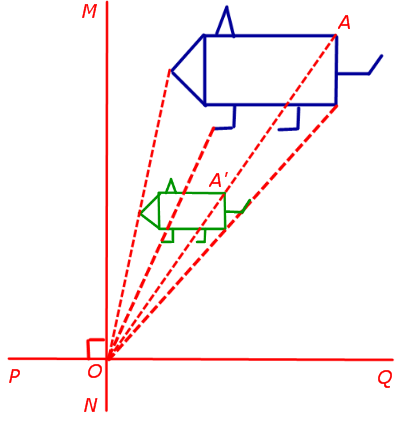
Хомотетия центриран при О и коефициентът К се нарича афинно преобразуване, в която произволна точка А в равнината минава точка А равнина ", които са изпълнени следните условия:

• точка А 'се намира на линията, AO;
• равенство

ако к> 0. След това точките А и лежат А 'от едната страна на точката О. ако к <0. то точки A и A' лежат по разные стороны от точки O (рис.11).

Забележка. Разгледаме две произволни перпендикулярни линии PQ и MN, пресичащи се в точка О. След хомотетия с център О и коефициент к съвпада с компресия (разширяване) в посоки PQ и MN с коефициенти равни на к. С други думи, дилатация е състава контракции (навяхване):

4. Превръщане на сходство с предварително определен фактор за претегляне

Сходство трансформация с коефициент сходство к наречен афинно преобразуване, представено чрез състав с хомотетно коефициент К и движение (фиг. 12).

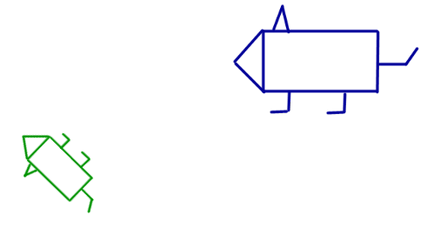
Класификация на афинни трансформации на равнината

Можете също така да се запознаят с учителите, разработени център за обучение "противовъзпалително" материали за обучение, за да се подготвите за изпита и OGE (ДПА) в областта на математиката.

За студенти, които искат да се подготвят добре и да мине изпита или OGE (ДПА) в областта на математиката, физиката или български език за най-висок резултат, на център за обучение "противовъзпалително" притежава