Комплексни числа Избрани проблеми

Федералната агенция ЗА ОБРАЗОВАНИЕ

ДЪРЖАВНА учебното заведение

ВИСШЕ ОБРАЗОВАНИЕ

"Воронеж държавен педагогически университет"

СТОЛ AGLEBRY и геометрия

Заключителни квалифицирани строителни работи

математиката специалност 050201.65

(С допълнителна специалност информатика 050202.65)

Изпълнено: ученик на 5-та година

2. Комплекс номера (избрани проблеми)

2.1. Комплексни числа в алгебрични форма .... ....... .......... ....

2.2. Геометричната интерпретация на комплексни числа ............ .. ...

2.3. Тригонометрични форма на комплексни числа

2.4. Прилагане на теорията на комплексните числа за решаване на уравненията на 3-ти и 4-ти степен ............... .. ...............................................................

2.5. Комплексни числа и параметри .......... ......................... ....

Програмата на математиката училище курс по теория на числата, въведена с примери на групи от естествени числа, числа, рационални, ирационални, т.е. на снимачната площадка на реални числа, образи, които изпълват целия недвижими линия. Но в 8 клас запасите от реални числа, не е достатъчно, за решаване на квадратно уравнение с отрицателна дискриминантен. Поради това е необходимо за попълване на запасите от реални числа, които използват сложни номера, за които корен квадратен от отрицателно число има смисъл.

Изборът на тема "Комплексни числа", тъй като темата на последната ми квалификационен работа е фактът, че концепцията за комплексно число се разширява знанията на цифрови системи на учениците за решаване на широк клас задачи като алгебричната и геометричната съдържанието на решаване на алгебрични уравнения на някаква степен и решаване на проблеми, свързани с параметри.

В тази теза работа преразглежда решение 82 х цели.

В първата част на основната част "комплексни числа" решения на проблемите с комплексни числа в алгебрични форма, определени операции на събиране, изваждане, умножение, делене, операция свързване на комплексни числа в алгебрични форма, степента на имагинерната единица, модулът на комплекс броя и описва обикновено изчисляване на корен квадратен от броя комплекс.

Във втората част на проблема решен в геометрична интерпретация на комплексни числа или вектори като точки в комплекс равнина.

В третата част се занимава с операции на комплексни числа в тригонометрични форма. Формула използва: DeMoivre и добив на основата на комплекс номер.

Четвъртата част е посветена на решаване на уравненията на 3 и 4 клас.

В решаването на проблемите на последната част на "комплексни числа и параметри" се използват и обезопасен информация, дадена в предишните части. Глави задачи поредица е посветена на определянето на семействата на линии в комплексната равнина, определена от уравнения (неравенства) с параметъра. Като част от упражнението трябва да се реши уравнението с параметър (над C). Има работни места, където комплекс променлива отговаря едновременно на няколко условия. Отличителна черта на решаване на проблемите на този раздел е да се намали повечето от тях към разтвора на уравнения (неравенства, системи) на втора степен, ирационално, тригонометрични, с параметър.

Функция, представяне на материала на всяка част е за въвеждане начални теоретични основи и впоследствие тяхното практическо приложение при решаване на проблеми.

В края на тезата е даден списък на използвана литература. Повечето от тях са доста подробна и достъпно очертава теоретичния материал обсъдени някои проблеми и решения са дадени практически задачи за самоопределение. Интересно на източници, като например:

1. Gordienko NA Belyaeva ES Firstov VE Serebryakov IV Комплексни числа и техните приложения: Учебник. [10]. Материал учебник е представена под формата на лекции и практически упражнения.

2. Имате Shkliarsky NN Chentsov Yaglom IM Избрани проблеми и теореми на елементарна математика. Аритметика и алгебра. [21] В книгата 320 съдържа задачи, свързани с алгебра и теорията на аритметични номера. По своята същност тези предизвикателства се различават значително от стандартните задачи училище.

2. Комплекс номера (избрани проблеми)

2.1. Комплексни числа са алгебрично

Решението на много проблеми в математиката, физиката се свежда до решаване на алгебрични уравнения, т.е. уравнения на формата

,

където a0. А1. ..., един са реални числа. Затова изучаването на алгебрични уравнения е един от най-важните въпроси в областта на математиката. Например, истинските корени на квадратното уравнение не оказва отрицателно дискриминантен. Най-простият като уравнение е уравнение

.

С цел това уравнение има решение, е необходимо да се разшири набора от реални числа, като се свързва с него корена на уравнението

.

Ще означаваме този корен чрез

. По този начин, по дефиниция,

,

.

Тя се нарича имагинерна единица. С него и с чифт реални числа

подготвени експресия на формата

.

Полученият израз се нарича комплексни числа, тъй като те съдържат както на реални и въображаеми части.

По този начин, комплексни числа се наричат ​​израз на формата

,

- реални числа, и

- символ задоволяване

Той призова реалната част на комплексно число

- имагинерната част. За използват техните наименования символи

,

.

Комплекс номера на формата

Те са реални числа, а оттам и на множество комплексни числа се състои от набор от реални числа.

Комплекс номера на формата

нарича чисто въображаемо. Две сложни номера на формата

каза, че е равен, ако те са реални и въображаеми части, т.е. ако равенства

,

.

Алгебрична въвеждане на комплексни числа ви позволява да извършвате операции по тях от обикновените правила за алгебра.

Сумата на две комплексни числа

е сложен номер

.

.

Писане на ненулева комплексно число Z като

Това се нарича тригонометрични форма на комплексно число Z. Броят R се нарича модула на комплексно число Z, и броя на # 966; това се нарича аргумент на комплексно число и е означен Argz.

Тригонометрични форма на комплексно число - (формула Ойлер) - експоненциална форма на комплексно число:

.

В комплексно число Z има безкрайно много аргументи: ако # 966; 0 - всеки аргумент на Z, след това останалата част може да се намери като се използва формулата

.

За комплексно число

аргумент и тригонометрични форма не се засича.

По този начин, не е нула аргумент на комплексно число

е всяко решение на системата:

стойност # 966; аргумента на комплексно число Z, което отговаря на неравенства

, Той призова главницата и определена argz.

Аргументи Argz и argz, свързани с

(5) е следствие от системата (3), така че всички аргументи на комплексното число

удовлетворява уравнението (5), но не всички разтвори # 966; Уравнение (5) са броят на аргументи Z.

Основната стойност на аргумента на ненулева комплексно число

се изчислява по формулата:

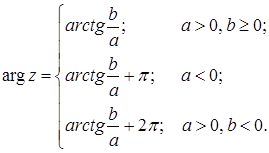
Формула на умножение и деление на комплексни числа в тригонометрични форма са както следва:

Когато издигането естествен мощност на комплекс броя използва DeMoivre формула:

формула се използва при екстрахиране на корените на комплексно число: