Как да си намерим по посока на основата на пирамидата
Предизвикателства за изчисляване на основата на пирамидата е в проблем книгата по геометрия, а голяма част. Много зависи от това, което gemoetricheskaya фигура се крие в основата, както и от това, което е дадено в проблема.
ще трябва
- - изготвяне оборудване;
- - книга в клетка;
- - Синиш;
- - Питагорова теорема;
- - калкулатор.
инструкция
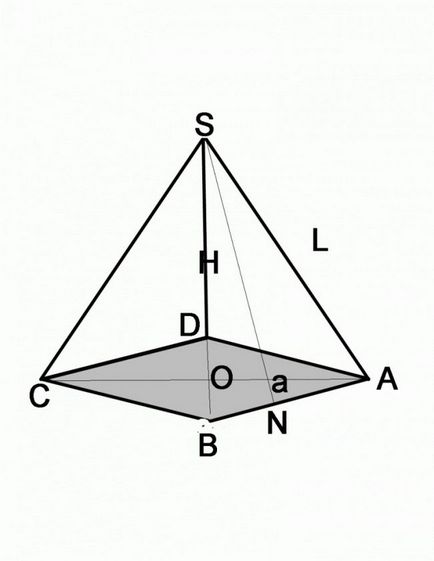
В училище разбира геометрия занимава главно на пирамидата, в основата на която е правилен многоъгълник, тоест такава, в която всички страни са равни. Проекцията на върха на пирамидата съвпада с центъра на основата. Начертайте пирамида, чиято база е равностранен триъгълник. могат да бъдат посочени условия:
- дължина на страничните ръбове на пирамидата, и ъгъл на ръба между страничната стена и osnovaniem-
- дължина на страничните ръбове и височина на борда bounda-
- дължина и височина на страничните ръбове на пирамидата.
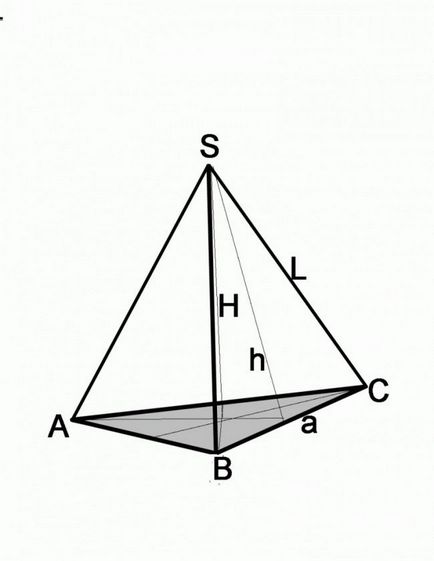
Ако знаете страничен ръб и ъгълът, проблемът е решен малко по-различно. Припомнете си, че всеки от тях представлява странична повърхност на пирамидата, чиято база е равностранен многоъгълник. Това е равнобедрен триъгълник. Прекарайте си височина, която е и ъглополовящата и медианата. Това е базовата страна половин / 2 = L * Коза, и където - базовата страна на пирамидата, L - дължина на ръба. За да разберете размера на базовата страна, това е достатъчно, за резултата, умножена по две.

Ако проблемът не се има предвид височината на страничните повърхности и ръбове дължина, се към основата на Питагоровата теорема. Странично лицето в този случай е известен височина на хипотенуза -s един от краката. За продължителността на второто рамо, е необходимо да се изважда от квадрата на хипотенузата квадрат втория крак, т.е. (а / 2) 2 = L2-H2, където - страна на основата, L - дължината на страничната повърхност, Н - височина на страничната стена.
В този случай, трябва да се извърши допълнително строителство, за да могат да работят на тригонометричните функции. Дадени са страничния ръб на L и Н височината на пирамидата, който свързва върха на пирамидата с база центъра. От височината на точката на пресичане на равнината на основата провежда сегмент свързване че точка на един от ъглите на основата. Сега имате правоъгълен триъгълник, хипотенузата, която е страничен ръб на един от краката - височината на пирамидата. Според тези данни, е лесно да се намери реванша на триъгълника, че е достатъчно на един квадратен шкаф L изважда квадрата на Н. височина Какво ще се случи след това зависи от това какъв вид форма е в основата.
Не забравяйте свойствата на равностранен триъгълник. Това е ръст е ъглополовящи и медиани. На пресечната точка, те са разделени на две. Това означава, че се оказва, че сте намерили половината от височината на основата. За улеснение на изчисление изпълнява всичките три височини. Вие ще видите, че сегмент, квадратна от дължината на които вече са открили, е хипотенузата на правоъгълен триъгълник. Премахване на корен квадратен. Знаеш ли, и остър ъгъл - 30 °, тъй като тази констатация половината от основата няма да е трудно, като се използват косинус теорема.
За пирамиди, чиито база е редовен четириъгълник, алгоритъмът ще бъде един и същ. Ако изваждате квадрата на страничните ръбове на квадрата на височината на пирамидата, да получите квадрат база половината диагонално. Премахване на корена, вземи размер на диагонала, който също е хипотенузата на равнобедрен правоъгълен триъгълник. Размерът на всеки от краката получите питагорова теорема, синус или косинус.