Как да сгънете хартията и я стигнем до Луната
Познаване на принципите на геометрична прогресия ни помага в ежедневието, от начисляването на лихвата по депозита, до скорост обучение на разпространение на епидемии. Също така, геометричната прогресия е в сърцето на известния парадокс, предизвикателни нашето разбиране за безкрайност.
Вземете лист вестник. Колко пъти да ви го сгънете наполовина? В реалния свят, не повече от седем пъти (опитайте да го себе си). Но нека си представим, че можем да сложим този лист толкова пъти, колкото искаме. Така че, ако се постави лист хартия само за 45 пъти, дебелината на слоя ще бъде толкова висока, че ще стигнем до Луната.
Нека да видим защо.
Да предположим, дебелина вестник лист 0.001 cm Ако огънати листови половини, дебелината се удвоява, и ще бъде 0.002 cm и с всяко следващо добавяне на половината от дебелината ще menyatsyav съответствие с последователността: .. 0,001 см, 0,002 см, 0,004 см, 0,008 см, 0,016 cm , 0,032 см ...
Сгъваеми листа на половина десет пъти. получаваме дебелина вестник на 1 см х 10 -3 * 2 10 или 1024, вижте, това е малко повече от един сантиметър. Необходимо е да се определят 17 пъти - не е проблем - поведат с 1 см х 10 -3 17 * 2 = 131 см, височина на средната хобит.
Шегите са повече, сега сериозно.
Сгънете тридесет пъти - почти десет километра (1 см х 10 -3 * 2 30). На тази височина самолетите летят! Четиридесет пъти - почти 11 000 км (1 cm х 10 -3 40 2 *). Хюстън има разлика! На тази височина орбита спътници в орбита: 43 пъти: 87 961 km, 44 пъти: 175921километра, 45 пъти: 351 844 км. Спри! Стигнали сме до Луната! Ако добавите лист хартия още един път, а след това можем да се върнем на Земята!
Този вид се нарича експоненциален растеж (експонат - показател). Неговата "експлозивен" природа контрастира с "бавен" линия и увеличение на мощността.
Номерата на последователността, получена от примера на вестник, образуват геометрична прогресия.
Геометрична прогресия - числова последователност б 1. b2. b3. където всеки последователни номера, започващи с втория се формира от предходните, като се умножава с определен брой Q (знаменател прогресия). В този случай, b1 ≠ 0 и р ≠ 0, в противен случай просто се нули последователност.
където п - цяло число.
Моля, обърнете внимание, да се знае всичко за експоненциално, е необходимо само три параметъра: стойността на първия елемент В1. прогресия Q, и броя на членовете п. В примера от първоначалната дебелина на хартията лист служи като първия елемент, както и факта, че чрез добавяне на половина на листа вестник неговата дебелина е удвоил, което ни дава стойност Q на = 2. Като се има предвид, че всяка прогресия елемент може да бъде представен като млрд = b1 * р ( п-1):
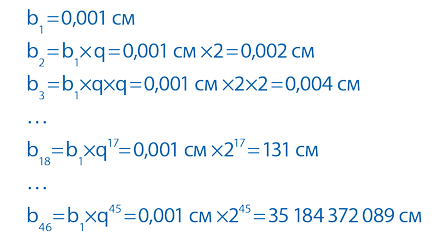
Както в случая с аритметична прогресия, че понякога е необходимо да се изчисли сумата на всички елементи от прогресия. Нека да направим един малък трик. Пишем уравнението, както следва, и след това се изважда второто уравнение от първата:
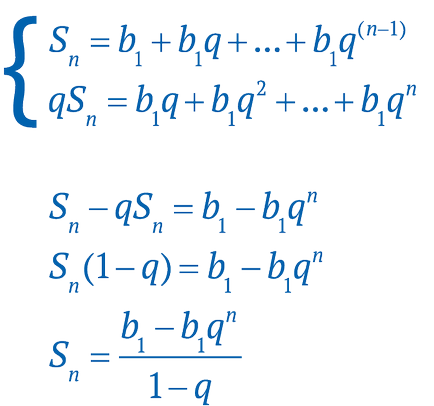
По този начин, ние получаваме формулата за изчисляване на сумата от краен брой геометрични елементи.
Геометрична прогресия е в основата на известния парадокс, предизвикателни нашето разбиране за безкрайност.
И какво, ако елементите в развитието на безкраен брой? Можем ли тогава се изчисли сумата на тази прогресия? Поведение експоненциално, и определя размера на прогресия р. И за почти всички р стойности нищо необичайно се случи, сумата от безкраен брой геометрични елементи не води до нещо ограничено. Това означава, че дисперсията, ако на езика на математиката.
Въпреки това, случаят, когато геометрична прогресия има безкраен брой елементи и знаменател е по-малко от единица (р<1 ) представляет особый интерес.
Интуицията ни казва, че сумата от безкраен брой положителни елементи трябва да бъде, добре, най-малко, да бъде безкраен. Вярно ли е това? На този въпрос отразява drevnegrecheskiyfilosof Zenon Eleysky, в бъдеще, тези мисли са станали основа за така наречения парадокс дихотомия парадокс или разделяне на две.
След продуктивен ден за размисъл, Зенон реши да ходи в парка, който се намира близо до дома му. Да приемем, че разстоянието да паркира една километра, а Зенон е със скорост 1 км / ч. Колко време е необходимо да се разходите?
Това са аргументите на Зенон. За да достигне до парка, първо трябва да отиде по средата - ½ км, нали? Това отнема половин час. Веднага след като е стигнал до средата на пътя, той ще трябва да мине през половината от оставащото разстояние - ¼ км. А това от своя страна ще се ¼ часа. На следващо място, това ще бъде направено това отново и отново. И може да продължи по този начин завинаги.
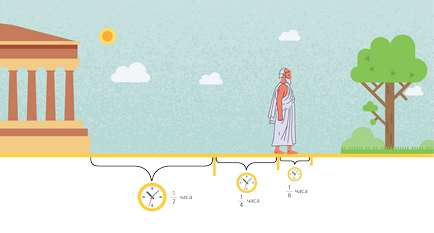
Е, колко време Zeno ще отиде в парка? За да отговорим на този въпрос, трябва да добавите до всички периоди, които са били изразходвани за всяка част от пътуването си. Проблемът обаче е, че като безкраен брой части!
Моля, имайте предвид, че следващия мандат на последователността увеличава количеството на:
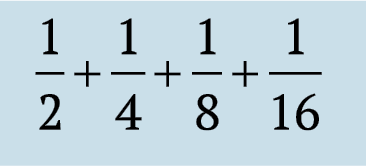
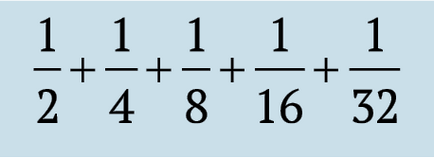
което от своя страна е по-малко от
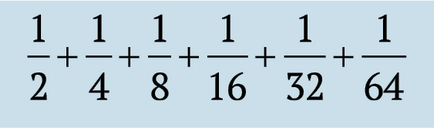
и така нататък. Това е нашата сума с всеки следващ елемент се увеличава и броят на членовете става безкрайно голяма, както е в нашия случай, сумата ще продължи да расте до безкрайност. Следователно, на разходка в парка отнема безкрайно количество време, с други думи, той никога не стига до парка!
Това е парадокс. От една страна, ние се занимаваме с ясна обосновка на Зенон, който твърди, че всяко движение е невъзможно, но от друга страна - ние можем да се изправи и да се разходите до хладилника. Първата мисъл, която се проявява - абсурд!
Но мотивите ум Зенон заета математици и философи в продължение на хиляди години, че се задълбочават разбирането на безкрайност и приемственост.
Къде е грешката в логиката на Зенон? Като част от математически модел за изчисляване на движението на разходката е лесно. Наистина, времето за пътуване - е разстояние, разделено на скоростта, следователно, приблизителното време, разходки - един час.
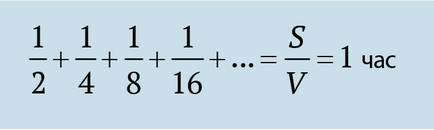
Както се оказа по-късно, математика, има моменти, когато това е възможно да обобщим безкраен брой елементи, и да получите окончателен отговор. Това е, както казват математиците, последователността клони. В нашия случай, безкрайно количество времеви интервали е равен (клони към) един час.
Както видяхме, безкрайно последователността, получена от Zeno е геометрична прогресия. И сумата на тази прогресия е конвергентна. Обърнете внимание на общ знаменател на развитието? Тя е равна на ½. Оказва се, че когато Q> -1 р<1 сумма бесконечной геометрической прогрессии сходится. Давайте вспомним формулу для конечной прогрессии и переделаем ее для бесконечного случая.
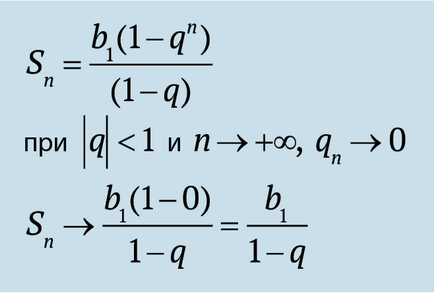
Обобщавайки, искам още веднъж да привлека вниманието ви към факта, тъй като изборът на прогресия р определя поведението на геометрична прогресия. От експоненциален растеж на експоненциално разпадане. От пътуване до Луната върху парче хартия и да се толкова малка стойност, че сумата им, дори и безкраен, няма значение.