Двойната задача - изготвянето на правила - линейното програмиране
Представя правилата за вземане на двойна проблеми. Се считат за симетричен, асиметричен и смесени двойки. Анализирани примери за съставяне на двойните проблеми.
Dual или конюгирана линейното програмиране проблем имат свойството, че решения от една от задачите, които можете да получите други задачи. Тук ще разгледаме правилата за съставяне на двойна проблеми.
Symmetric двоен проблем
Да разгледаме проблема с линейното програмиране с неотрицателни променливи и неравенството в системата от ограничения на следния вид:
(1.1);
(1.2)
Тук. има някои числа. Всички системи линия (1.2) е неравенството на знака.
Двойното Проблемът е:
(2.1);
(2.2)
Ето, всички от линията на система (2.2) е неравенството на знака. Матрицата коефициенти на системата за ограничение (2.2) е транспонирана матрица на системата (1.2). Той включва редове и колони. Двойното Проблемът е променлива. Всички променливи са неотрицателни.
Оригиналният проблема (1) е често по-нататък директно предизвикателство и проблем (2) - двойна. Ако започнете да приемате този проблем (2), а след това (2) ще ръководи задача и задачата (1) - двойна. Задачи (1) и (2) се наричат симетрични двойни задачи.
По този начин, симетричен двоен проблем може да се формира само ако всички променливи на първоначалния проблем и неотрицателна системата за ограничение не съдържат уравнения. Ако ви търсят за максимум целевата функция, неравенството трябва да се преобразува в формата. Ако търсите най-малко, неравенствата, трябва да бъдат преобразувани във формата. За смяна на знака, трябва да умножите двете страни на неравенството от -1.
Пример на симетричен двоен проблем
Като се има предвид линейното програмиране проблем:
;
Създаване на двоен проблем.
Първоначалната Проблемът е задачата за намиране минимум. Ето защо, всички признаци на неравенството трябва да има. По първия и третия неравенства съдържат знака. ги умножава по 1:
Ние пренапише системата на ограничения, като ясно се посочва коефициентите на променливите:
Системни ограничения коефициент матрица има формата:
Транспонират тази матрица. Това означава, че първия ред може да се запише като първата колона, на втория ред може да се запише като втората колона, на третия ред може да се запише като третата колона.
Двойното Проблемът е:
;
Асиметричен двоен проблем
Предизвикателството за максимално
Помислете каноничната Задачата на линейното програмиране с максимална неотрицателни променливи и равнопоставеност на ограничения на системата:
(3.1);
(3.2)
Тук. има някои числа. Всички системи линии (3.2) са равенства. Всички променливи са неотрицателни.
Двойното Проблемът е:
(4.1);
(4.2)
Ето, всички от линията на система (4.2) е неравенството на знака. Матрицата коефициенти на системата за ограничение (4.2) е транспонирана матрица на системата (3.2). Двойното Проблемът е променлива. Променливи могат да бъдат или положителни или отрицателни.
За разлика асиметрични проблеми двойка (3) и (4) на симетричен двойка (1) и (2), че ограниченията на системата (3.2) съдържа само равенство, и в системата (4.2) няма условия nonnegativeness променливи.
Задачата поне
А сега да разгледаме каноничен Задачата на линейното програмиране до минимум:
(5.1);
(5.2)
Двойното Проблемът е:
(6.1);
(6.2)
ограничение система (6.2) е различно от (4,2), които са признаци на неравенство.
Комуникация с симетричен чифт двойни проблеми
Ние показваме, че небалансирани проблеми двойка (3) - (4) могат да бъдат получени от симетрични двойки (1) - (2).
Така че, предполагам, че имат пряко проблем с целевата функция
(3.1)
и ограниченията на системата
(3.2)
Всеки уравнение може да бъде представен от две неравенства:
Неравенства с признаци размножават от 1:
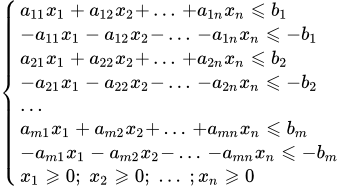
Системата има неравенство ограничения.
От (1) - (2) получаваме двоен проблем:
;
двоен проблем има не-отрицателни променливи:
.
Лесно е да се види, че тези променливи са част от проблема във формата на различия
.
Ние правим това заместване
.
Тъй като и двете. променливите могат да бъдат както положителни, така и отрицателни.
И ще получим двоен проблем (4):
(4.1);
(4.2)
Ако вземем за първоначалния проблем (4), извършване на всички стъпки в обратен ред, ние се получи двоен проблем (3).
По същия начин може да бъде проблем (5) за получаване на двойна проблема (6) и проблемът на (6) за получаване на двойна проблема (5).
Смесен проблем
А сега да разгледаме смесен проблема.
Да предположим, че имаме пряк проблем (1) до максимум, в система, която ограничава ред I-Я е равенство. След това двойната проблема има формата (2), с едно изключение - променливата може да бъде или положителен или отрицателен. Това означава, че няма ограничение.
Същото нещо се случва, ако имаме пряк проблем (2) най-малко в системата, която ограничава ред I-Я е равенство. Двойното проблем има формата (1) с едно изключение - променливата може да бъде от всеки знак.
Да предположим сега, че имаме пряк проблем (1) до максимум, но няма ограничение. Това означава, че променливата може да бъде положителен или отрицателен. Тогава двоен проблем има форма (2), с едно изключение - ти ред ограничение система е равенство.
И накрая, да предположим, че имаме пряк проблем (2) до минимум, но няма ограничение. Тогава двоен проблем има формата (1) с едно изключение - ти ред ограничение система е равенство.
Всичко това ни позволява да се формулира правилата за вземане на двойна проблеми.
Правила за вземане на двойна проблеми
1. За първоначалния проблем до максимум, всички неравенство ограничения на системата на произвежда:
.
За първоначалния проблем до минимум, всички неравенството намалява с:
.
Ако искате да смените знака, след това умножете двете страни на неравенството от -1.
2. Уверете се двоен проблем по същия начин, както за симетрични задачи по двойки.
3. Ако първоначалният проблем, та ограничения на линията на системата е равенство, тогава ние зачеркнете състоянието на не-негативност тата променлива на двойната проблема.
4. Ако първоначалният проблем, няма условие, без негативизъм за променливата I-Я. в-ти ред на двойния проблем смяна на знака на неравенството на знака за равенство.
Пример на смесения двойна проблема
Като се има предвид линейното програмиране проблем:
;
Създаване на двоен проблем.
Целевата функция има свободен член 5. За да го донесе на формата (2.1), ще се въведе една променлива и добавяне на половете. Тогава проблемът става:
Този проблем е проблем за намиране на минимум. Ето защо, всички признаци на неравенството трябва да има. Трети неравенства съдържат знак. Ето защо, ние го умножете по -1:
Ние пренапише системата на ограничения, като ясно се посочва коефициентите на променливите:
Системни ограничения коефициент матрица има формата:
Транспонират тази матрица. Това означава, че първия ред може да се запише като първата колона, на втория ред може да се запише като втората колона, и така нататък.
Ние построи двойна проблема за двете симетрични двойка.
;
Както и при първоначалното проблем 1, 2 и четвърти ред са ограниченията на уравненията на системата, променливите в двойна проблема. и може да има някакъв знак. Non-отрицателни променлива е просто. Ето защо, в условията на не-негативност на променливите са в следния формат:
.
Както при първоначалното проблема и променливи могат да имат произволни знаци, 3-ти и 4-ти ред системни ограничения на двойния проблем са равенства.
По този начин, двоен проблем има следния вид:
;
От четвъртата уравнението. Замяна на променливата и неговата стойност, умножим третия ред от -1.