Диагонал аксиален на формулата на цилиндър

Забележка. Тази част на урока с проблемите на геометрията (раздел геометрия). Ако трябва да се реши проблема с геометрия, което не е тук - пише за него във форума. В проблеми SQRT () функция се използва вместо "квадратен корен" символ, който SQRT - квадратен корен символ, и в скоби експресията под радикал.

Задача.
Намери обща площ на цилиндъра, ако диагонала на своя раздел аксиален, равна на 8 см, е образувателна на цилиндъра стойност под ъгъл от 30 градуса.

Решение.

Тъй като AC = 8 см, а ъгълът ACD = 30 °, след това
CD = AC COS 30 °

Обяснение. Правоъгълна - ACD триъгълник. Съответно, CD / AC = защото ∠ACD върху свойствата на тригонометрични функции в правоъгълен триъгълник. Стойността, определена от масата.

По същия начин,
AD = AC
AD = 8 * 1/2 = 4

Къде радиус база цилиндър, равна на 4/2 = 2 см

Площта на основата на цилиндъра, съответно, е равна на
S1 = πR 2 = 4π

Площта на страничната повърхност на цилиндъра е равна на площта на неговото сканиране - продуктът на основния кръг, а дължината на височината на цилиндъра. Това е:
S2 = 2πRh = 2π * 2 * 4√3 = 16π√3

Общата площ на цилиндъра е равна на:
S1 + S2 = 4π + 16π√3

Ученикът (97), затворен преди 5 години

Диагонала аксиален разрез на цилиндъра и образува А = Н цилиндър образуваща ъгъл а. Намери странична повърхност и обема на цилиндъра на

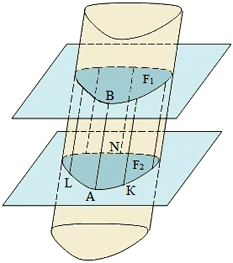
Аксиална част на цилиндъра в общия случай - правоъгълник. Сегмент свързваща точките на кръгове, перпендикулярна на равнината на бази и бази, наречена цилиндъра. Дължината на генератора е равно на височината на цилиндъра. Формула площ и обем в учебника.

Цилиндричната повърхност - на повърхността, образувана от движение на линията (във всяка позиция, наречена образуваща) по крива (наречена употреба), така че линията винаги остава успоредна на първоначалната си позиция.

Директен AB - формиране;

крива AKNLA - водач.

Endless цилиндър - тяло, граничеща с цилиндрична повърхност.

Цилиндър - геометрична тяло ограничена от цилиндрична повърхност и две паралелни равнини, които се пресичат.

Част от повърхността на цилиндъра, ограничена от цилиндрична повърхност, наречена странична повърхност цилиндър.

Височината на цилиндъра е разстоянието между равнините на нейните основи.

Друга част граничи с успоредни равнини - etoosnovaniya цилиндър.

Сегмент AB - формиране;

Фигури F1 и F2 - база.

• база равен;
• образуване на паралелни и равна.

Страничната повърхност на цилиндъра е равна на формиране сечение, перпендикулярно на периметъра на продукта.

Обемът е продукт на всеки цилиндър на височината на база площ: V = SH.

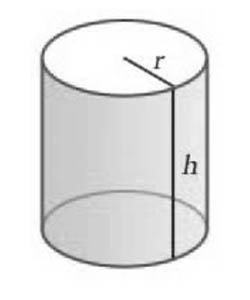
Цилиндърът, които са перпендикулярни на основата и се образуват кръгове се нарича прав кръгов цилиндър (често, а след това - само цилиндъра).

Право кръгов цилиндър може да бъде получена чрез въртене на правоъгълник около една от неговите страни.

Radiusomtsilindra нарича основата му радиус.

Оста на цилиндъра се нарича права линия, минаваща през центъра на своята база. оста на цилиндрите е успоредна на генераторите.

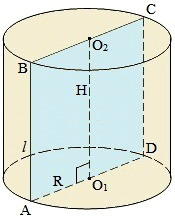
Аксиален разрез на цилиндъра се нарича цилиндър сечение равнина, минаваща през оста си. Аксиален разрез на цилиндъра (прав кръгов цилиндър) е правоъгълник.

АО1 - радиус на цилиндъра;

AB. CD - формиране на цилиндър;

AB. CD. O1 O2 - височината на цилиндъра;

ABCD - осово сечение на цилиндъра.

Страничната повърхност на прав кръгов цилиндър с височина, равна на продукт база обиколката: Sbok = 2πRH.

Пълен повърхност на цилиндъра се изчислява по формулата: Sn + = Sbok 2Sosn = 2πR (Н + К).

За обема на прав кръгов цилиндър е вярно: V = 2 πR Н.

Цилиндърът е геометрично тяло, ограничена от две успоредни равнини и с цилиндрична повърхност.

Цилиндърът включва странична повърхност и две основи. Формула площ на повърхността на цилиндър включва отделна изчисляване на квадратна основа и страничната повърхност. Тъй като основата на цилиндъра са равни, тогава общата площ ще се изчислява съгласно формулата:

Пример за изчисляване на площта цилиндър ние ще се грижат научите всички необходими формули. За да започнете, ние се нуждаем от формула поле на основата цилиндър. Тъй като в основата на цилиндър е кръг, ние трябва да се прилагат.
Ние помним, че в тези изчисления се използват постоянно = 3.1415926, се изчислява като съотношение на дължината на окръжността към нейния диаметър. Този номер е математическа константа. Пример за изчисляване на цилиндър базовата площ, ние също ще разгледаме малко по-късно.

Формула площ на страничната повърхност на цилиндъра е продукт на дължината в основата си височина:

По този начин, като се използва формула областта на базите и страничните повърхностни форми, ние може да намери общата повърхност на цилиндъра.
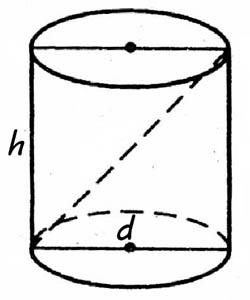
Аксиална част на цилиндъра е правоъгълник, в който двете страни са равни височина и диаметър на цилиндъра.

Формула аксиално сечение на цилиндъра се получава от формулата за изчисление:

• Въвеждане на концепцията на цилиндричната повърхност на цилиндъра и неговите компоненти (база образуващ ос, височина радиус);
• Помислете за различните случаи на напречните сечения на цилиндъра;
• Обучение за извършване на необходимите фигури;
• Помислете типичните задачи по този въпрос;
• Решаване на проблема с изпита.

Вид на урока. комбинирани.

2. пред работата с класа:

- Дайте примери за елементи от живота около себе си, като формата на цилиндър (слайд 4)

- Какво известния геометрични фигури намерени в цилиндъра?

- Име формула обиколка.

- Име на формула областта на кръг.

3. Изследване на нов материал:

1. Обмислете варианта за получаване на цилиндър (слайд 5. 6);
2. На рисунката покаже своите цилиндрови елементи (слайд 7);
3. Равенство в тетрадки рисуване цилиндър;
4. Zoom сечение равнина на цилиндъра (слайд 8);
5. За да се въведе понятието равностранен цилиндър.

4. Осигуряване на новия материал:

1. Среща на предизвикателствата на завършен чертеж (слайд 9), умения за изграждане на напречното сечение:

1. Превъртете раздел цилиндър равнина, успоредна на земята и да получите своята област, ако базовата радиус, равен на 5 см.
2. Превъртете аксиално сечение на цилиндъра и да получите своята област, ако височината на цилиндъра е 10 см. База радиус от 2,1 см.

2. Независима работа (Изберете правилния отговор) (тест) (слайд 10):

1. . Ако равностранен радиус база цилиндър на 2.5 cm осовото площ е равна на:
   а) 25 cm 2;
   б) 225 cm 2;
   а) 6,25π cm 2;
   ж) 225π cm2.
2. Ако аксиално сечение на цилиндъра - с квадратна площ от 36 cm2, площта на основата на цилиндъра е равна на:
   а) 10π cm 2;
   б) 3π cm 2;
   а) 9π cm 2;
   ж) 36π cm2.

3. Решение № 522 учебник геометрия (плъзнете 11):

Диагонал аксиално сечение на цилиндъра е 48 см. Ъгълът между диагонала и образуващата на цилиндъра е 60˚. Търсене за:

а) височината на цилиндъра;
б) радиусът на цилиндъра;
в) база площта на цилиндър.

А правоъгълен паралелепипед окръжност около цилиндър база, чийто радиус е равен на 5. Обемът на паралелепипеда е равно на височината на цилиндър 400. намери.