Основни тригонометрични идентичности, на изхода на формулите

В тази статия, ще разгледаме подробно основните тригонометрични самоличността. Основни тригонометрични идентичности са равни, за установяване на връзка между синус, косинус, тангенс и котангенс на ъгъла и позволяват да се намери някой от тези известни тригонометрични функции през друга.

Веднага се изброят основните тригонометрични самоличността, които анализират в тази статия. Напиши ги в таблицата по-долу дава деривация на тези формули и да даде необходимото обяснение.

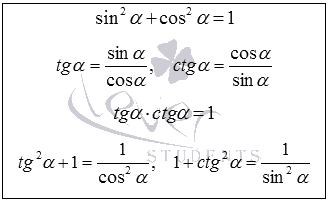
Навигация в страниците.

Връзката между синуса и косинуса на ъгъла

Това е, от особен интерес е равенство, което дава името на основните тригонометрични самоличността.

Преди доказване на Питагоровата тригонометрични идентичност, се получава формулировка си: сумата от квадратите на синус и косинус на ъгъла е идентично равен на единица. Сега го докаже.

Позовавайки се на единица кръг. Да предположим, че началната точка А (1, 0) след завъртане на ъгъл в точка А1. От определенията на синуса и косинуса на точката А1 има координатите. Освен това, А1 се намира на единица кръг, следователно, координатите трябва да отговарят на единичната окръжност, която има форма х 2 + Y 2 = 1. Това означава, че трябва да има равенство. Това доказва, Питагоровата тригонометрични идентичност за всички ъгли на въртене.

Равенството често се нарича питагорова теорема в тригонометрията. Нека илюстрираме тази точка.

Вземете единичната окръжност. Завъртане на начална точка А (1, 0) около точката O под ъгъл. Нека точка А след завъртането става А1 точка (х, у). Капка от точка А1 А1 Н перпендикулярна на линията Ox.

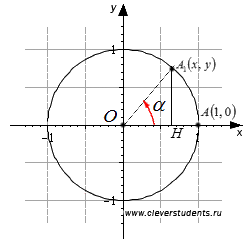
Да разгледаме правоъгълен триъгълник OA1 H. ясно се вижда в това, че дължината на краката А1 Н и ОН съответно абсцисата и ординатата модул А1 точка. т.е. | А1 Н | = | у | и | ОН | = | х |. OA1 и дължината на хипотенузата е равен на радиуса на единица кръг, т.е. | OA1 | = 1. Питагорова теорема ни позволява да напишете равенството | A1 H | 2 + | ОН | 2 = | OA1 | 2. можем да бъде пренаписана, както | у | 2 + | х | 2 = 1 или 2, Y 2 + 2 х = 1. Но, по дефиниция, и след това от уравнението у 2 + х 2 = 1, можем да преминем към равенство.

Питагоровата тригонометрични идентичност често се използва при конвертиране на тригонометрични изрази. Тя позволява на сумата от квадратите на синус и косинус на ъгъла на устройството заменя. Поне част от основния тригонометрични самоличността се използва в обратен ред: единица се заменя със сумата от квадратите на синуса и косинуса на ъгъл.

Tangent и котангенс през синуса и косинуса

Идентичности, свързващи тангента и котангенс с синус и косинус на ъгъла на един вид и веднага следват определенията на синус, косинус, тангенс и котангенс. Наистина, по дефиниция, е задължително ординатата у, косинус е абсцисата X, допирателната е съотношението на ординатата за абсциса, т.е., едно легло е съотношението на абсцисата на ординатата, т.е..

Поради това очевидно идентичност и често се определи допирателната и котангенс не изразява чрез съотношението на абсцисата и ординатата, а съотношението на синуса и косинуса. Така че тангентата на ъгъл е отношението на синуса на косинуса на ъгъла, и котангенс - отношението на синуса на косинус.

В заключение този раздел трябва да се отбележи, че самоличността и имат място за всички ъгли, в който членовете на тези тригонометрични функции са смислени. Така че формулата е валидна за всяка различна от (в противен случай знаменателят е нула и разделението на нула, ние не се определи), и формулата - за всички, освен когато Z - всяко число.

Връзката между допирателната и котангенс

Дори и по-очевидни тригонометрични идентичности в сравнение с предишните две, е идентичността, свързващ тангенс и котангенс на ъгъла на виждане. Ясно е, че това се отнася и за всеки ъгъл, различен от, в противен случай или допирателната или котангенс не е определена.

Доказателство за формулата е много проста. По дефиниция, и, където е. Това е възможно да се извърши доказателството и малко по-различно. Така харесва, тогава.

Така че, допирателна и котангенс на ъгъла, под който те имат смисъл, има реципрочен брой.

Тангенсът и косинус, синус и котангенс

И накрая, ние стигаме до последните две от основните тригонометрични самоличността. Те свързват допирателната и косинус и синус и котангенс на ъгъла.

Ето формулировка им: сумата от квадрата на допирателната на ъгъла и броя единици равни обратна на квадрата на косинуса на ъгъла, и сумата от квадрата на устройството и котангенс на ъгълът е равен на реципрочната стойност на квадрата на синуса на ъгъла.

Заключение Тези формули могат да се извършват, като се започне от основните тригонометрични идентичности вида. Ако разделим двете страни на това уравнение от (в този случай, разбира се, трябва да е различен от нула), ние получаваме формулата. Ако и двете страни са разделени от (това трябва да е различна от нула), стигаме до идентичност.

По този начин, на идентичността се отнася и за всяка отделна от, и идентичност - във всеки друг, отколкото.